What Percent Of 4 Is 3
News Co
Apr 03, 2025 · 4 min read
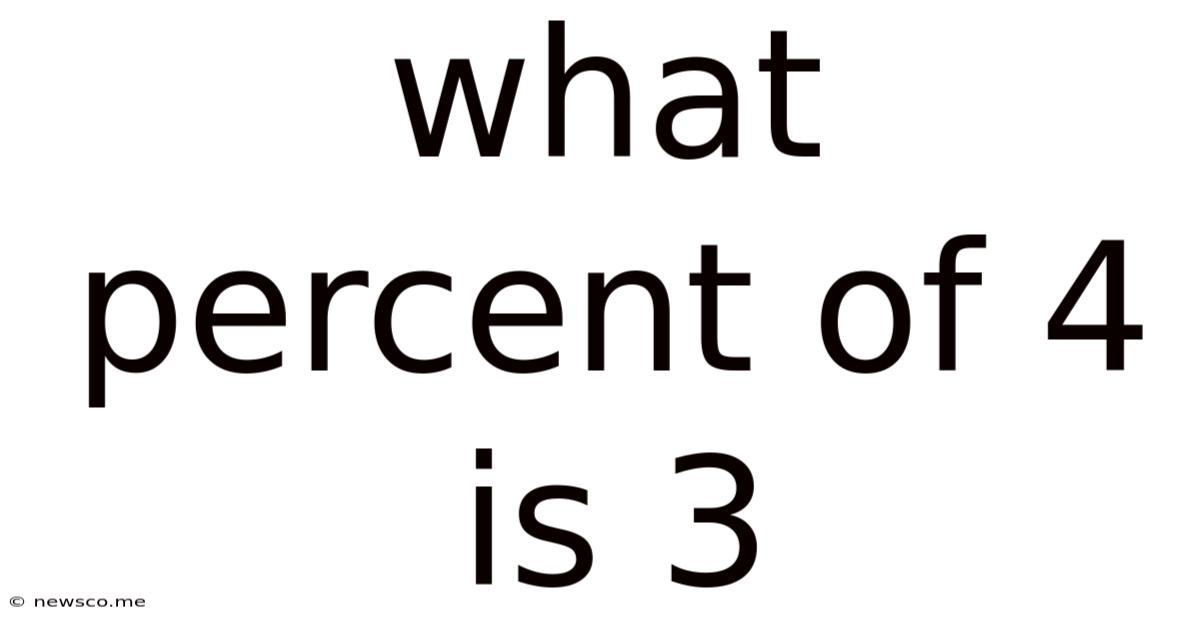
Table of Contents
What Percent of 4 is 3? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article delves deep into the seemingly simple question, "What percent of 4 is 3?", providing a comprehensive explanation not just of the solution but of the underlying concepts and various methods for solving similar percentage problems. We'll explore different approaches, including the formula method, the proportion method, and even a visual representation to solidify your understanding.
Understanding the Problem: Deconstructing "What Percent of 4 is 3?"
The question "What percent of 4 is 3?" asks us to find the percentage value that represents 3 out of 4. In simpler terms, we need to determine what fraction 3/4 represents as a percentage. This is a classic percentage problem, and mastering its solution provides a strong foundation for tackling more complex percentage calculations.
Method 1: The Formula Method – A Direct Approach
This method utilizes the fundamental percentage formula:
Percentage = (Part / Whole) x 100
Where:
- Part: Represents the value we're interested in (in this case, 3).
- Whole: Represents the total value (in this case, 4).
Let's apply this to our problem:
Percentage = (3 / 4) x 100
Percentage = 0.75 x 100
Percentage = 75%
Therefore, 3 is 75% of 4.
Method 2: The Proportion Method – Setting up a Ratio
This method involves setting up a proportion to solve for the unknown percentage. We can represent the problem as a ratio:
3/4 = x/100
Where 'x' represents the unknown percentage.
To solve for 'x', we cross-multiply:
4x = 300
x = 300 / 4
x = 75
Therefore, 3 is 75% of 4.
Method 3: The Decimal Method – Converting Fractions to Percentages
This method leverages the understanding that percentages are simply fractions expressed as hundredths. We start by converting the fraction 3/4 to a decimal:
3 ÷ 4 = 0.75
To convert this decimal to a percentage, we multiply by 100:
0.75 x 100 = 75%
Hence, 3 is 75% of 4.
Visualizing the Solution: A Pie Chart Representation
A visual representation can greatly enhance understanding, especially for those who prefer a more intuitive approach. Imagine a pie chart divided into four equal slices. If three of these slices represent a value of 3, then each slice represents 3/4 = 0.75 units. Since a whole pie chart represents 100%, three slices out of four represent (3/4) * 100% = 75%.
Extending the Concept: Solving Similar Problems
The principles outlined above are applicable to a wide range of percentage problems. Let's consider some variations:
Example 1: What percent of 10 is 7?
Using the formula method: Percentage = (7/10) x 100 = 70%
Example 2: What percent of 25 is 15?
Using the proportion method: 15/25 = x/100 => 25x = 1500 => x = 60%
Example 3: 12 is 60% of what number?
In this case, we need to rearrange the formula: Whole = (Part / Percentage) x 100. Substituting the values, we get: Whole = (12 / 60) x 100 = 20.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
- Retail and Sales: Calculating discounts, sales tax, and profit margins.
- Finance: Determining interest rates, returns on investment, and loan payments.
- Statistics: Analyzing data, interpreting survey results, and understanding probabilities.
- Science: Expressing concentrations, measuring changes, and representing experimental results.
- Everyday Life: Tipping in restaurants, understanding nutritional information, and comparing prices.
Common Mistakes to Avoid
While percentage calculations seem straightforward, several common errors can lead to inaccurate results:
- Incorrect Formula Application: Ensure you're using the correct formula and substituting values accurately.
- Decimal Point Errors: Pay close attention to decimal points during calculations to avoid significant errors.
- Confusion Between Part and Whole: Always clearly identify the "part" and the "whole" in the problem.
- Percentage vs. Decimal Conversion: Accurately convert between decimals and percentages by multiplying or dividing by 100.
Mastering Percentages: Practice and Resources
The key to mastering percentage calculations is consistent practice. Solve a variety of problems, starting with simple ones and gradually increasing the complexity. Numerous online resources, including educational websites and interactive calculators, can assist in your learning journey. Focus on understanding the underlying concepts rather than just memorizing formulas.
Conclusion: Beyond the Simple Calculation
The seemingly simple question, "What percent of 4 is 3?", serves as a gateway to a broader understanding of percentage calculations and their extensive applicability. By mastering the different methods and avoiding common pitfalls, you’ll be well-equipped to tackle a vast array of percentage-related problems encountered in various fields, ultimately enhancing your problem-solving skills and critical thinking abilities. Remember, the more you practice, the more confident and proficient you will become in handling percentages.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 4 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.