What Percent Of 5 Is 3
News Co
Mar 31, 2025 · 5 min read
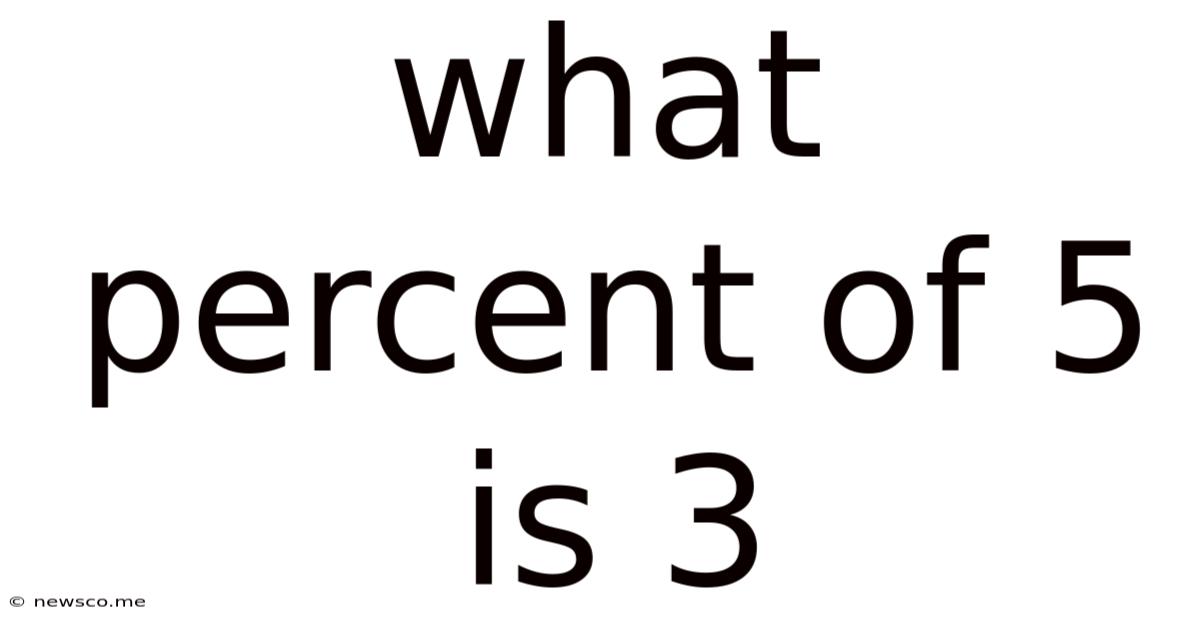
Table of Contents
What Percent of 5 is 3? A Comprehensive Guide to Percentage Calculations
Percentages are fundamental to everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. Knowing how to calculate percentages is a crucial skill, and one of the most common questions involves finding what percentage one number represents of another. This comprehensive guide will delve into how to determine what percent of 5 is 3, explaining the process step-by-step and providing various methods to solve similar problems. We'll also explore practical applications and related concepts to solidify your understanding.
Understanding the Fundamentals of Percentages
Before we dive into solving "What percent of 5 is 3?", let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. For instance, 50% means 50 out of 100, which can also be written as 50/100 or 1/2 (one-half).
Understanding this basic principle is key to solving percentage problems. We often need to translate real-world situations into mathematical equations to find the solution.
Method 1: Using the Proportion Method
This method is a classic approach to solving percentage problems. We set up a proportion, which is an equation stating that two ratios are equal. In our case, we want to find the percentage (let's call it 'x') that 3 represents of 5. We can set up the proportion as follows:
3/5 = x/100
This equation states that the ratio of 3 to 5 is equal to the ratio of x (our unknown percentage) to 100. To solve for x, we can cross-multiply:
3 * 100 = 5 * x
300 = 5x
Now, we divide both sides by 5 to isolate x:
x = 300/5
x = 60
Therefore, 3 is 60% of 5.
Method 2: Using Decimal Conversion
This method involves converting the fraction 3/5 into a decimal and then multiplying by 100 to express it as a percentage.
First, we divide 3 by 5:
3 ÷ 5 = 0.6
Next, we multiply the decimal by 100 to convert it to a percentage:
0.6 * 100 = 60
Again, we find that 3 is 60% of 5. This method is often quicker for simple calculations.
Method 3: Using the Formula
A more general formula for calculating percentages can be expressed as:
Percentage = (Part / Whole) * 100
In our problem:
- Part: 3
- Whole: 5
Substituting these values into the formula:
Percentage = (3 / 5) * 100 = 0.6 * 100 = 60%
This formula provides a systematic approach that can be applied to any percentage problem, making it a valuable tool for various applications.
Practical Applications: Real-World Examples
Understanding percentage calculations is crucial in many real-world situations. Here are some examples:
-
Discounts: A store offers a 20% discount on an item originally priced at $50. To calculate the discount, we find 20% of $50: (20/100) * $50 = $10. The discounted price is $50 - $10 = $40.
-
Sales Tax: If the sales tax is 6% and the price of an item is $25, the sales tax amount is (6/100) * $25 = $1.50. The total price including tax is $25 + $1.50 = $26.50.
-
Grade Calculations: If you scored 27 out of 30 on a test, your percentage score is (27/30) * 100 = 90%.
-
Financial Analysis: Understanding percentage changes in stock prices, interest rates, or profit margins is essential for making informed financial decisions. For example, if a stock increases from $10 to $12, the percentage increase is ((12-10)/10) * 100 = 20%.
Expanding Your Understanding: Related Concepts
Beyond basic percentage calculations, there are related concepts to explore:
-
Percentage Increase/Decrease: This involves calculating the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100. -
Percentage Points: This is often confused with percentage change. Percentage points represent the absolute difference between two percentages. For instance, if interest rates increase from 2% to 5%, the increase is 3 percentage points, not a 150% increase.
-
Compound Interest: This involves earning interest on both the principal amount and accumulated interest. Understanding compound interest is crucial for long-term investments and loans.
-
Statistical Analysis: Percentages are frequently used in statistical analysis to represent proportions, probabilities, and other key metrics.
Mastering Percentage Calculations: Tips and Tricks
To become proficient in percentage calculations:
-
Practice Regularly: The more you practice, the more comfortable you'll become with the different methods and formulas.
-
Use Different Methods: Experiment with the proportion method, decimal conversion, and the general formula to find the approach that works best for you.
-
Check Your Answers: Always double-check your calculations to ensure accuracy.
-
Use Calculators: While mental calculations are helpful, using a calculator can save time and reduce errors, particularly for more complex problems.
-
Understand the Context: Always pay attention to the context of the problem to ensure you're applying the correct formula and interpreting the results correctly.
Conclusion: The Power of Percentage Understanding
The question "What percent of 5 is 3?" might seem simple, but it highlights the importance of understanding percentage calculations. This seemingly basic skill has far-reaching applications across various fields. By mastering different methods and understanding related concepts, you'll be well-equipped to tackle more complex percentage problems and apply this knowledge to various real-world scenarios, making you more confident and competent in your numerical abilities. Remember to practice regularly and explore the numerous applications of percentages to truly grasp their significance and utility.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 5 Is 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.