What Percent Of 50 Is 15
News Co
Mar 20, 2025 · 4 min read
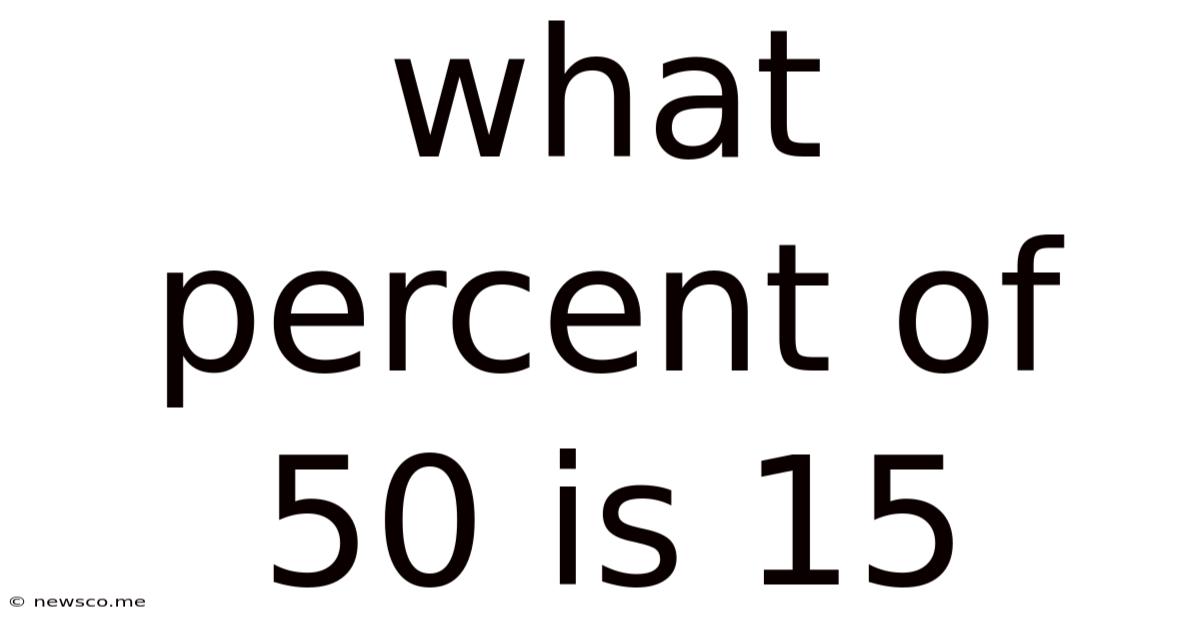
Table of Contents
What Percent of 50 is 15? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve into the question, "What percent of 50 is 15?", providing a detailed explanation of the calculation process, exploring different approaches, and offering practical examples to solidify your understanding. We'll also examine related concepts and explore how to tackle similar percentage problems efficiently.
Understanding the Problem: What Percent of 50 is 15?
The question "What percent of 50 is 15?" asks us to find the percentage representing the ratio of 15 to 50. In essence, we're looking for a number (expressed as a percentage) that, when multiplied by 50, results in 15. This is a classic percentage calculation problem, and we can solve it using several methods.
Method 1: Using the Formula
The most straightforward way to solve this problem is to use the basic percentage formula:
Part / Whole = Percentage / 100
In this case:
- Part: 15 (the value we're interested in)
- Whole: 50 (the total value)
- Percentage: This is what we need to find (let's represent it as 'x')
Substituting these values into the formula, we get:
15 / 50 = x / 100
To solve for 'x', we can cross-multiply:
15 * 100 = 50 * x
1500 = 50x
Now, divide both sides by 50:
x = 1500 / 50
x = 30
Therefore, 15 is 30% of 50.
Method 2: Using Decimal Conversion
This method involves converting the fraction representing the ratio into a decimal and then multiplying by 100 to express it as a percentage.
First, express the ratio as a fraction:
15/50
Now, simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (5):
15/50 = 3/10
Next, convert the fraction to a decimal by dividing the numerator by the denominator:
3 ÷ 10 = 0.3
Finally, multiply the decimal by 100 to express it as a percentage:
0.3 * 100 = 30%
So, again, we find that 15 is 30% of 50.
Method 3: Using Proportions
Proportions offer another effective approach to solving percentage problems. We can set up a proportion to represent the relationship between the part, the whole, and the percentage:
15/50 = x/100
Cross-multiplying gives us:
15 * 100 = 50 * x
1500 = 50x
Solving for x:
x = 1500 / 50
x = 30
Thus, using proportions confirms that 15 is 30% of 50.
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in various real-life scenarios. Here are some examples demonstrating the application of this skill:
-
Discounts: A store offers a 30% discount on an item originally priced at $50. The discount amount is 30% of $50, which is $15 (as calculated above). The final price would be $50 - $15 = $35.
-
Taxes: If a sales tax is 6%, and you buy something for $50, the tax amount would be 6% of $50. This calculation would require you to determine 6% of 50, using the same methods described above, and then adding the tax amount to the original price.
-
Grade Calculations: If you score 15 out of 50 on a test, your percentage score is 30%. This helps you understand your performance relative to the total possible marks.
-
Data Analysis: Percentage calculations are extensively used in analyzing data in various fields like finance, marketing, and healthcare. They help visualize and compare proportions within datasets.
Solving Similar Percentage Problems
The methods outlined above are easily adaptable to solve similar percentage problems. For instance, if you need to find what percent of 75 is 25, you would simply substitute 25 as the part and 75 as the whole into the percentage formula or use the other methods shown above. The key is to identify the part, the whole, and the unknown percentage (or sometimes, the unknown part or whole).
Advanced Percentage Calculations: Finding the Whole or the Part
While the primary focus was finding the percentage, let's briefly explore finding the whole or the part when other elements are known.
- Finding the Whole: If you know the percentage and the part, you can find the whole. For example: "15 is 30% of what number?" This can be solved by setting up an equation:
15 = 0.3 * x
x = 15 / 0.3
x = 50
- Finding the Part: If you know the percentage and the whole, you can find the part. For example: "What is 30% of 50?" This is solved by multiplying the percentage (as a decimal) by the whole:
0.3 * 50 = 15
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is an invaluable skill applicable across various domains. The methods outlined in this article—using the formula, decimal conversion, and proportions—provide versatile tools for solving percentage problems effectively. By practicing these techniques and applying them to real-world examples, you'll build a solid foundation in percentage calculations and confidently tackle a wide range of quantitative challenges. Remember the fundamental relationship between the part, the whole, and the percentage, and you'll be well-equipped to solve any percentage problem you encounter. The key to mastering percentage calculations lies in understanding the underlying principles and practicing consistently.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 50 Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.