What Percent Of 500 Is 150
News Co
May 07, 2025 · 5 min read
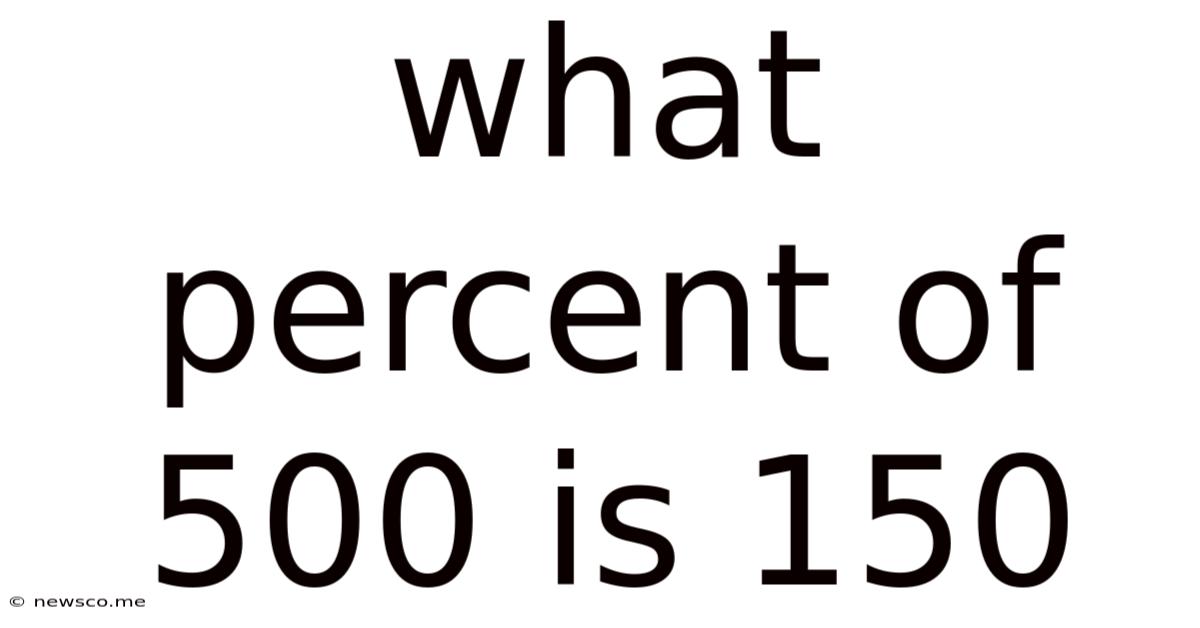
Table of Contents
What Percent of 500 is 150? A Deep Dive into Percentages and Their Applications
Determining what percentage 150 represents of 500 is a fundamental concept in mathematics with broad applications across various fields. This seemingly simple calculation underlies many real-world scenarios, from calculating discounts and tax rates to understanding statistical data and analyzing financial performance. This comprehensive guide will not only answer the question directly but also explore the underlying principles, provide multiple methods for solving the problem, and delve into the practical significance of percentage calculations.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Percentages are a convenient way to represent proportions and comparisons, making them easily understandable and widely used.
Key Concepts:
- Part: The specific amount we're interested in (in our case, 150).
- Whole: The total amount we're comparing the part to (in our case, 500).
- Percentage: The ratio of the part to the whole, expressed as a number out of 100.
Calculating the Percentage: Three Methods
There are several ways to determine what percentage 150 represents of 500. Let's explore three common methods:
Method 1: The Formula Approach
The most straightforward method uses a simple formula:
(Part / Whole) x 100 = Percentage
Substituting our values:
(150 / 500) x 100 = 30%
Therefore, 150 is 30% of 500.
Method 2: Using Proportions
This method leverages the concept of ratios and proportions. We can set up a proportion:
150/500 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
500x = 15000
x = 15000 / 500
x = 30
Therefore, 150 is 30% of 500.
Method 3: Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100:
150/500 = 0.3
0.3 x 100 = 30%
Again, we find that 150 is 30% of 500.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios. Here are some examples:
1. Financial Calculations:
- Discounts: A store offers a 30% discount on a $500 item. The discount amount is (30/100) x $500 = $150. The final price is $500 - $150 = $350.
- Interest Rates: Calculating simple interest involves determining a percentage of a principal amount. If you invest $500 at a 6% annual interest rate, you'll earn (6/100) x $500 = $30 in interest after one year.
- Taxes: Sales tax, income tax, and property tax are all calculated as percentages of a specific amount.
- Investment Returns: Analyzing investment performance often involves calculating percentage changes in portfolio value. If your $500 investment grows to $650, your return is ((650-500)/500) x 100 = 30%.
2. Statistical Analysis:
- Data Representation: Percentages are used to represent proportions within datasets, making it easier to compare and understand trends. For example, if 150 out of 500 respondents in a survey prefer a particular brand, this translates to 30% preference.
- Probability: Percentages are used to express probabilities. For instance, if there's a 30% chance of rain, it means that out of 100 similar situations, it's likely to rain in approximately 30.
3. Everyday Life:
- Tip Calculation: Calculating a tip at a restaurant often involves determining a percentage of the bill. A 20% tip on a $50 meal is (20/100) x $50 = $10.
- Sales Conversions: Businesses use percentages to track the effectiveness of their sales campaigns, measuring conversion rates (the percentage of website visitors who make a purchase).
- Grade Calculation: Many grading systems use percentages to represent a student's performance relative to the total possible points.
Beyond the Basics: More Complex Percentage Problems
While the example of finding what percent 150 is of 500 is relatively straightforward, percentage calculations can become more complex. Consider these scenarios:
- Finding the Whole: If 30% of a number is 150, what is the number? This requires reversing the formula: (150 / 30) x 100 = 500.
- Finding the Part: What is 25% of 500? This involves calculating (25/100) x 500 = 125.
- Percentage Increase/Decrease: Calculating percentage change involves finding the difference between two values and expressing it as a percentage of the original value. For example, if a value increases from 500 to 650, the percentage increase is ((650-500)/500) x 100 = 30%.
- Compound Interest: Compound interest calculations involve calculating interest on both the principal and accumulated interest from previous periods, leading to exponential growth.
Mastering Percentages: Tips and Tricks
Developing proficiency in percentage calculations requires practice and understanding the underlying principles. Here are some helpful tips:
- Memorize Common Percentages: Familiarize yourself with common percentage equivalents of fractions (e.g., 1/4 = 25%, 1/2 = 50%, 3/4 = 75%).
- Use a Calculator: For more complex calculations, using a calculator can save time and ensure accuracy.
- Practice Regularly: Work through various percentage problems to solidify your understanding and build your skills.
- Break Down Complex Problems: Divide complex problems into smaller, manageable steps.
- Check Your Answers: Always review your calculations to ensure accuracy.
Conclusion: The Importance of Percentage Understanding
Understanding percentages is a crucial skill applicable across various aspects of life. From navigating financial transactions and interpreting statistical data to making informed decisions in everyday situations, the ability to calculate and understand percentages empowers you to make sense of the numerical world around you. Mastering this fundamental concept provides a solid foundation for tackling more complex mathematical and real-world challenges. The simple calculation of determining what percentage 150 is of 500—30%—serves as a gateway to a deeper understanding of this essential mathematical tool.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 500 Is 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.