What Percent Of 60 Is 12
News Co
Apr 02, 2025 · 4 min read
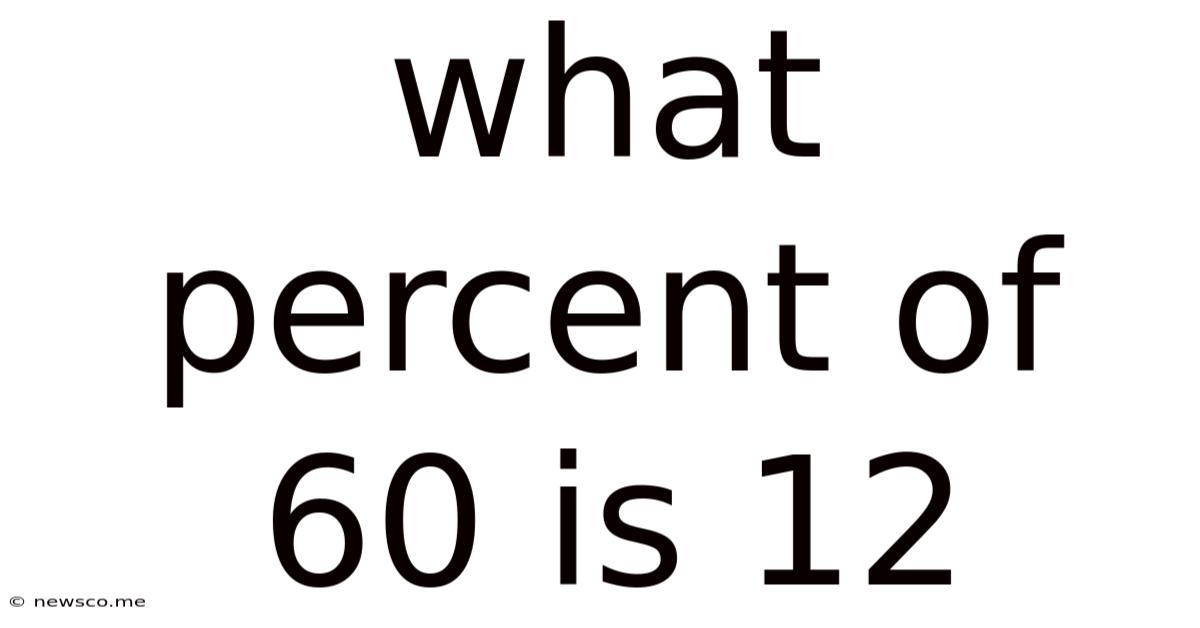
Table of Contents
What Percent of 60 is 12? A Comprehensive Guide to Percentage Calculations
Finding out what percentage one number represents of another is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial data. This article dives deep into the question, "What percent of 60 is 12?", explaining the solution in multiple ways, exploring related concepts, and providing practical examples to solidify your understanding.
Understanding Percentages
Before tackling the problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100". For instance, 50% means 50 out of 100, which simplifies to ½ or 0.5.
Key Concepts:
- Part: This represents the smaller portion of the whole. In our example, 12 is the part.
- Whole: This is the total or complete amount. In our case, 60 is the whole.
- Percentage: This is the fraction of the whole expressed as a number out of 100. This is what we need to find.
Method 1: Using the Formula
The most straightforward method to solve "What percent of 60 is 12?" involves using the basic percentage formula:
(Part / Whole) x 100 = Percentage
Let's plug in our values:
(12 / 60) x 100 = Percentage
- Divide the part by the whole: 12 / 60 = 0.2
- Multiply the result by 100: 0.2 x 100 = 20
Therefore, 12 is 20% of 60.
Method 2: Setting up a Proportion
Another way to solve this problem is by setting up a proportion. A proportion is an equation that states two ratios are equal. We can set up a proportion like this:
12 / 60 = x / 100
Where 'x' represents the percentage we need to find.
To solve for 'x', we can cross-multiply:
12 * 100 = 60 * x
1200 = 60x
Now, divide both sides by 60:
x = 1200 / 60
x = 20
Again, we find that 12 is 20% of 60.
Method 3: Using Decimal Equivalents
Percentages can also be expressed as decimals. To use this method:
- Divide the part by the whole: 12 / 60 = 0.2
- Convert the decimal to a percentage: Multiply the decimal by 100. 0.2 x 100 = 20%
This confirms, once again, that 12 is 20% of 60.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world situations:
1. Retail and Sales:
- Discounts: A store offers a 25% discount on an item priced at $80. The discount amount is (25/100) * $80 = $20.
- Sales Tax: A 6% sales tax is applied to a $50 purchase. The tax amount is (6/100) * $50 = $3.
- Profit Margins: Businesses calculate profit margins as a percentage of their revenue to track profitability.
2. Finance and Investments:
- Interest Rates: Interest on loans and savings accounts is typically expressed as a percentage.
- Investment Returns: The return on investments is often stated as a percentage increase or decrease.
- Inflation: Inflation, the rate at which prices rise, is measured as a percentage.
3. Statistics and Data Analysis:
- Data Representation: Percentages are used to represent proportions within data sets, making it easier to visualize and understand trends.
- Surveys and Polls: Results from surveys and polls are frequently expressed as percentages to show the distribution of opinions or preferences.
- Probability: Probability, the likelihood of an event occurring, is often expressed as a percentage.
4. Everyday Life:
- Tip Calculation: Calculating a tip at a restaurant often involves determining a percentage of the total bill.
- Recipe Scaling: Adjusting ingredient quantities in a recipe often involves percentage calculations.
- Grade Calculation: Your final grade in a course might be calculated as a weighted percentage of different assignments and exams.
Expanding Your Understanding: More Complex Percentage Problems
While the "What percent of 60 is 12?" problem is relatively straightforward, understanding the fundamental principles allows you to tackle more complex percentage calculations. Here are a few examples:
- Finding the Whole: If 30% of a number is 15, what is the number? This requires rearranging the percentage formula.
- Finding the Part: What is 15% of 80? This involves direct application of the formula.
- Percentage Increase/Decrease: A value increases from 50 to 60. What is the percentage increase? This involves calculating the difference, dividing by the original value, and then multiplying by 100.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a valuable skill that extends far beyond the classroom. Whether you're managing your personal finances, analyzing data, or navigating everyday situations, understanding how to solve problems like "What percent of 60 is 12?" is an essential tool for success. By mastering the different methods explained in this article, and by practicing regularly, you can confidently tackle a wide range of percentage-related calculations with ease and accuracy. Remember the fundamental formula, (Part / Whole) x 100 = Percentage, and practice using the different approaches outlined above to solidify your understanding and build your confidence in tackling percentage problems of all types. The more you practice, the more intuitive and effortless these calculations will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.