What Percent Of 8 Is 20
News Co
Mar 27, 2025 · 4 min read
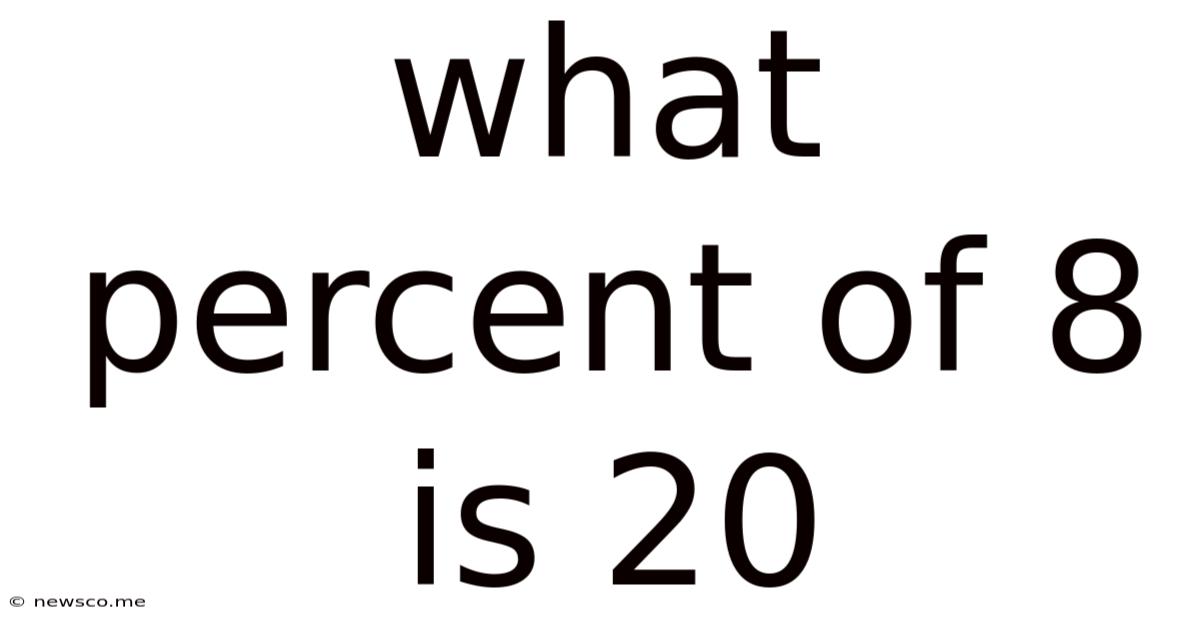
Table of Contents
What Percent of 8 is 20? Understanding Percentages and Proportions
This seemingly simple question, "What percent of 8 is 20?", delves into the fundamental concepts of percentages and proportions. While the answer might seem counterintuitive at first glance (since 20 is larger than 8), understanding the underlying mathematical principles is crucial for various applications in daily life, from calculating discounts and tax rates to analyzing data and understanding statistics. This comprehensive guide will explore multiple approaches to solving this problem, offering a deeper understanding of percentages and their applications.
Deconstructing the Problem: Percentages and Proportions
Before diving into the solution, let's clarify the core concepts:
-
Percentage: A percentage represents a fraction of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are a way to express a proportion relative to a whole.
-
Proportion: A proportion is a statement of equality between two ratios. In our case, we're looking for a proportion where one ratio represents the percentage (x/100) and the other ratio represents the relationship between 20 and 8 (20/8).
Method 1: Using the Percentage Formula
The most straightforward method to solve "What percent of 8 is 20?" involves using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this scenario:
- Part: 20 (the value we're comparing)
- Whole: 8 (the base value)
Substituting these values into the formula:
(20 / 8) * 100% = 250%
Therefore, 20 is 250% of 8.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion:
x/100 = 20/8
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
8x = 2000
Then, divide both sides by 8:
x = 250
Again, this confirms that 20 is 250% of 8.
Method 3: Understanding the Implication of a Percentage Greater Than 100%
The result, 250%, might seem unusual because percentages are often thought of as being between 0% and 100%. However, a percentage greater than 100% simply means that the "part" is larger than the "whole." In this context, 20 is more than 8, hence the percentage exceeds 100%. This concept is often encountered when dealing with growth, increases, or comparisons where one value surpasses another.
Real-World Applications of Percentages Greater Than 100%
Percentages exceeding 100% are commonly used in various real-world scenarios:
-
Financial Growth: If a company's profits increase from $8 million to $20 million, the percentage increase would be 250%.
-
Population Growth: If a town's population grows from 8,000 to 20,000, the population increase is 250%.
-
Price Increases: If the price of a product increases from $8 to $20, the price increase is 250%.
-
Data Analysis: In various statistical analyses, comparing changes over time or across different groups might result in percentages greater than 100%.
Expanding the Understanding: Variations on the Problem
Let's explore some related problems to solidify our understanding:
Problem 1: What is 250% of 8?
This is a direct application of the percentage formula:
(250/100) * 8 = 20
This confirms our previous findings.
Problem 2: 20 is what percent of 25?
Using the percentage formula:
(20/25) * 100% = 80%
This shows a percentage less than 100% because 20 is smaller than 25.
Problem 3: What number is 150% of 12?
Here, we solve for the "part":
(150/100) * 12 = 18
Practical Tips and Tricks for Solving Percentage Problems
-
Master the Formula: Familiarize yourself with the basic percentage formula: (Part/Whole) * 100% = Percentage.
-
Practice Regularly: Solving various percentage problems will enhance your understanding and problem-solving skills.
-
Use Proportions: Setting up a proportion is an alternative and effective method for solving percentage problems.
-
Check Your Answers: Always verify your solution by substituting the values back into the equation or using a different method to confirm your result.
-
Understand the Context: Consider the context of the problem. Percentages greater than 100% are perfectly valid in scenarios where the "part" is larger than the "whole."
Conclusion: Beyond the Numbers
This in-depth exploration of "What percent of 8 is 20?" extends beyond a simple mathematical calculation. It's about mastering the concepts of percentages and proportions, understanding their practical applications, and interpreting results, even when they might seem unexpected. By understanding these fundamental concepts, you'll be better equipped to tackle various percentage-related problems in your daily life, academic pursuits, and professional endeavors. The ability to confidently calculate and interpret percentages is a valuable skill with far-reaching implications.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 8 Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.