What Percent Of 90 Is 75
News Co
Mar 29, 2025 · 4 min read
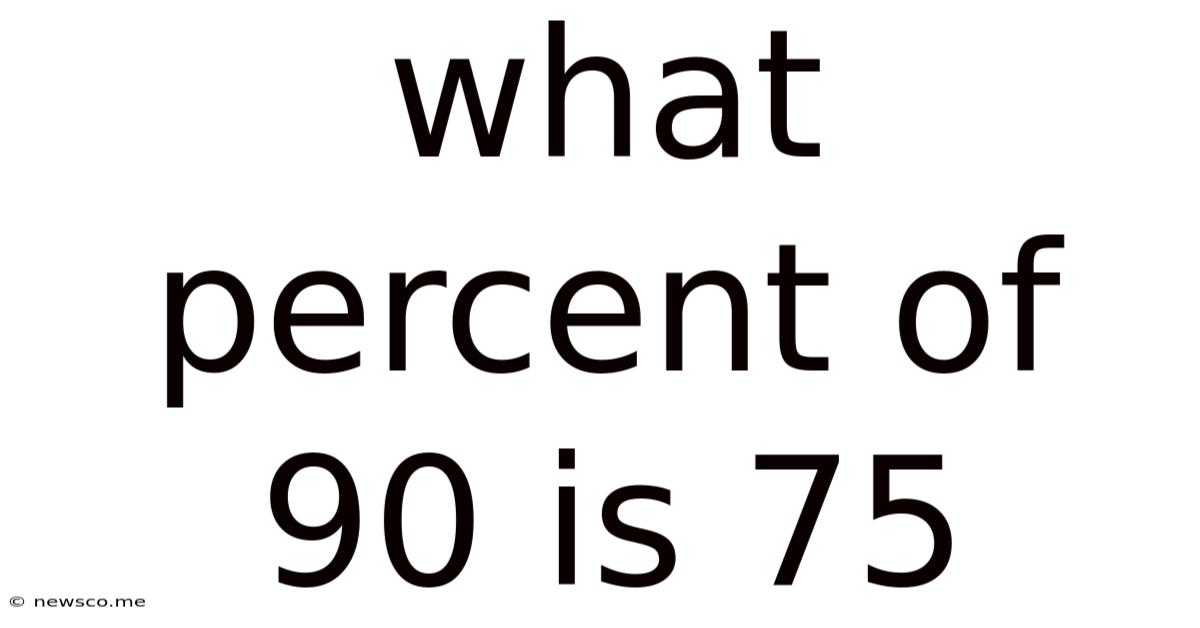
Table of Contents
What Percent of 90 is 75? A Comprehensive Guide to Percentage Calculations
Finding what percentage one number represents of another is a fundamental mathematical skill with broad applications in various fields, from everyday budgeting and shopping to complex scientific calculations and business analysis. This article will delve into the question, "What percent of 90 is 75?", providing a detailed explanation of the solution, exploring different methods of calculation, and demonstrating its relevance through real-world examples.
Understanding Percentages:
Before diving into the specific problem, let's establish a clear understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Method 1: Using Proportions
The most straightforward method to solve "What percent of 90 is 75?" involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the proportion:
x/100 = 75/90
Where 'x' represents the unknown percentage we're trying to find.
To solve for 'x', we cross-multiply:
90x = 75 * 100
90x = 7500
Now, divide both sides by 90:
x = 7500 / 90
x = 83.333...
Therefore, 75 is approximately 83.33% of 90. The recurring decimal indicates that the percentage is not exactly 83.33%, but rather an approximation. For most practical purposes, rounding to two decimal places is sufficient.
Method 2: Using the Formula
We can also solve this using a more direct formula:
Percentage = (Part / Whole) * 100
In our problem:
- Part: 75
- Whole: 90
Substituting these values into the formula:
Percentage = (75 / 90) * 100
Percentage = 0.8333... * 100
Percentage ≈ 83.33%
This formula directly calculates the percentage, offering a concise and efficient solution.
Method 3: Simplifying the Fraction
Before applying the formula, simplifying the fraction 75/90 can make the calculation easier. Both 75 and 90 are divisible by 15:
75/90 = (75 ÷ 15) / (90 ÷ 15) = 5/6
Now, converting the simplified fraction 5/6 to a percentage:
(5/6) * 100 ≈ 83.33%
This method showcases the importance of simplifying fractions to streamline calculations.
Real-World Applications:
The ability to calculate percentages is crucial in various scenarios:
-
Discounts: Imagine a store offering a discount on an item originally priced at $90. If the discounted price is $75, you can use this percentage calculation to determine the discount percentage (83.33%).
-
Grade Calculation: If a student scores 75 out of 90 on a test, this calculation determines their percentage score (83.33%).
-
Sales Analysis: Businesses use percentage calculations to track sales performance, comparing sales figures to targets or previous periods. For instance, if a business aimed for $90,000 in sales and achieved $75,000, the percentage of the target achieved is 83.33%.
-
Financial Planning: Percentages are essential in financial planning, such as calculating interest rates, tax deductions, and investment returns.
-
Scientific Research: Many scientific experiments and studies rely on percentage calculations to analyze data and draw conclusions.
Beyond the Basics: Further Exploration of Percentage Calculations
While the problem "What percent of 90 is 75?" provides a foundational understanding of percentage calculation, let's explore some related concepts:
1. Finding the Whole: If we know the percentage and the part, we can find the whole. For example, if 83.33% of a number is 75, we can find the whole number using the formula:
Whole = (Part / Percentage) * 100
Whole = (75 / 83.33) * 100 ≈ 90
2. Finding the Part: Similarly, knowing the percentage and the whole, we can determine the part. For example, if 25% of 90 is needed, we can calculate:
Part = (Percentage / 100) * Whole
Part = (25 / 100) * 90 = 22.5
3. Percentage Increase/Decrease: These calculations are frequently used to compare changes in values. For example, if a value increases from 75 to 90, the percentage increase is calculated as:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
Percentage Increase = [(90 - 75) / 75] * 100 ≈ 20%
Similarly, a percentage decrease can be calculated using the same formula but with the old value subtracted from the new value.
Advanced Applications and Tools:
For more complex percentage calculations involving multiple variables or large datasets, spreadsheets (like Microsoft Excel or Google Sheets) and statistical software packages can be highly effective tools. These programs offer built-in functions that automate percentage calculations, reducing the risk of errors and saving time.
Conclusion:
Determining "What percent of 90 is 75?" is a simple yet vital calculation. Mastering this skill and its variations opens doors to a wider understanding of percentages and their extensive applications across diverse fields. By understanding the different methods, formulas, and real-world applications of percentage calculations, you can confidently tackle similar problems and improve your analytical skills. Remember that practice is key, so explore different examples and apply these methods to enhance your proficiency. The ability to accurately calculate percentages is a valuable asset in both academic and professional settings.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 90 Is 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.