What Percentage Is 1/3 Of 100
News Co
Apr 12, 2025 · 4 min read
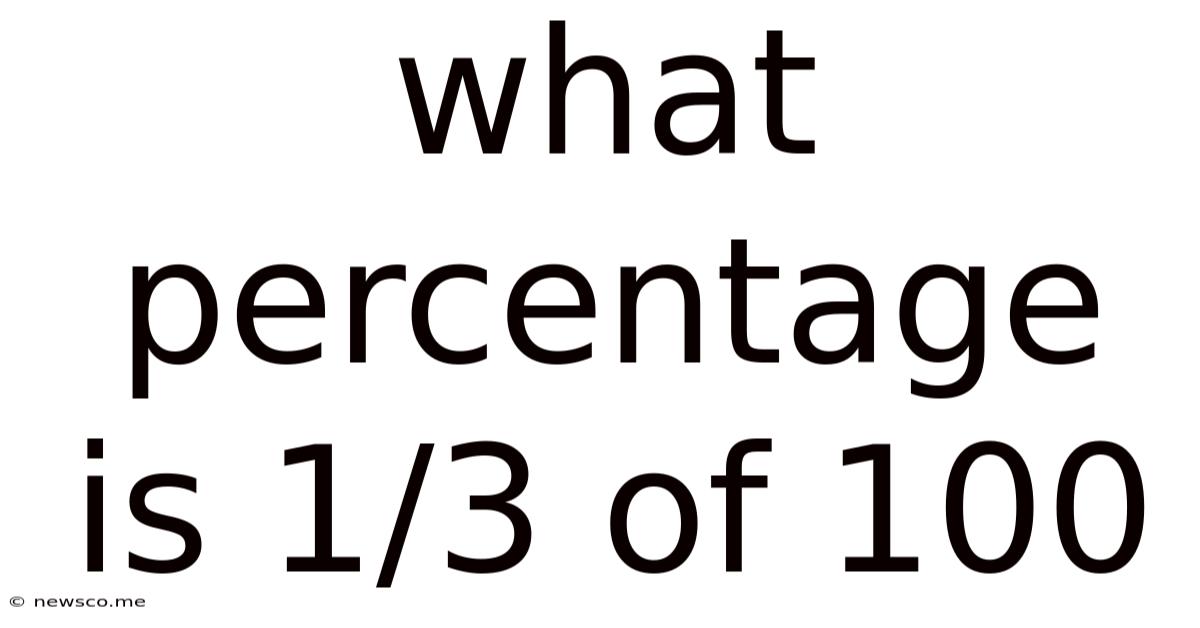
Table of Contents
What Percentage is 1/3 of 100? A Comprehensive Guide to Fractions, Decimals, and Percentages
Understanding fractions, decimals, and percentages is fundamental to many aspects of life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the question, "What percentage is 1/3 of 100?", providing a detailed explanation and exploring related concepts. We'll break down the process step-by-step, ensuring you grasp not just the answer but the underlying mathematical principles.
Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. In our case, 1/3 means one part out of three equal parts.
Visualizing 1/3
Imagine a pizza cut into three equal slices. 1/3 represents one of those slices. To understand what percentage 1/3 of 100 represents, we need to convert the fraction into a percentage.
Converting Fractions to Percentages
A percentage is a fraction where the denominator is always 100. To convert a fraction to a percentage, we need to find an equivalent fraction with a denominator of 100. There are two primary methods:
Method 1: Using Equivalent Fractions
To find an equivalent fraction with a denominator of 100, we ask ourselves: "What number, when multiplied by the original denominator (3), equals 100?" This isn't a whole number, which means we'll need to use decimals.
- We can set up a proportion: 1/3 = x/100
- To solve for x, we cross-multiply: 3x = 100
- Dividing both sides by 3: x = 100/3 ≈ 33.333...
Therefore, 1/3 is approximately equal to 33.33%.
Method 2: Converting to a Decimal First
Another way to convert a fraction to a percentage is to first convert the fraction to a decimal. We do this by dividing the numerator by the denominator:
- 1 ÷ 3 ≈ 0.333...
Next, we convert the decimal to a percentage by multiplying by 100:
- 0.333... × 100 ≈ 33.33%
Both methods lead to the same result: 1/3 of 100 is approximately 33.33%.
Calculating 1/3 of 100 Directly
We can also calculate 1/3 of 100 directly:
- (1/3) * 100 = 100/3 ≈ 33.33
This confirms our previous calculations.
The Importance of Understanding Recurring Decimals
Notice that the decimal representation of 1/3 (0.333...) is a recurring decimal. This means the digit 3 repeats infinitely. In practice, we round the decimal to a certain number of decimal places for practical purposes. In this case, we commonly round to two decimal places (33.33%), but the exact value is 33.333...%
Applications of Fractions, Decimals, and Percentages
The ability to convert between fractions, decimals, and percentages is crucial in many real-world situations:
- Retail Sales: Calculating discounts, sales tax, and profit margins.
- Finance: Understanding interest rates, loan repayments, and investment returns.
- Data Analysis: Interpreting statistical data presented as percentages.
- Cooking and Baking: Following recipes that use fractional measurements.
- Construction and Engineering: Making precise measurements and calculations.
Beyond the Basics: Working with More Complex Fractions
The principles discussed above can be extended to more complex fractions. For instance, let's consider calculating 2/5 of 100:
- Method 1 (Equivalent Fractions): 2/5 = x/100 => 5x = 200 => x = 40. Therefore, 2/5 of 100 is 40%.
- Method 2 (Decimal Conversion): 2 ÷ 5 = 0.4 => 0.4 × 100 = 40%.
Practical Examples
Let's explore some real-world scenarios that demonstrate the application of these concepts:
- Scenario 1: Sales Discount: A store offers a 1/3 discount on an item priced at $100. The discount amount is (1/3) * $100 = $33.33. The final price is $100 - $33.33 = $66.67.
- Scenario 2: Survey Results: A survey shows that 1/3 of 100 respondents prefer a particular product. This means 33.33% of respondents prefer the product.
- Scenario 3: Recipe Adjustment: A recipe calls for 1/3 cup of sugar, but you want to double the recipe. You would need 2/3 cup of sugar (2 * (1/3) = 2/3).
Conclusion
Understanding how to calculate percentages, especially from fractions, is a valuable skill. This guide has provided a step-by-step explanation of how to determine that 1/3 of 100 is approximately 33.33%, covering various methods and highlighting the importance of recurring decimals. Mastering these concepts will equip you to confidently tackle numerous mathematical problems in various aspects of your life. Remember to practice regularly to reinforce your understanding and build confidence in your mathematical abilities. By consistently applying these methods, you can accurately and efficiently solve percentage problems related to fractions, improving your problem-solving skills in both academic and real-world contexts. The more you practice, the easier these conversions will become, solidifying your understanding of the fundamental relationship between fractions, decimals, and percentages.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percentage Is 1/3 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.