What Percentage Of 20 Is 8
News Co
Mar 20, 2025 · 5 min read
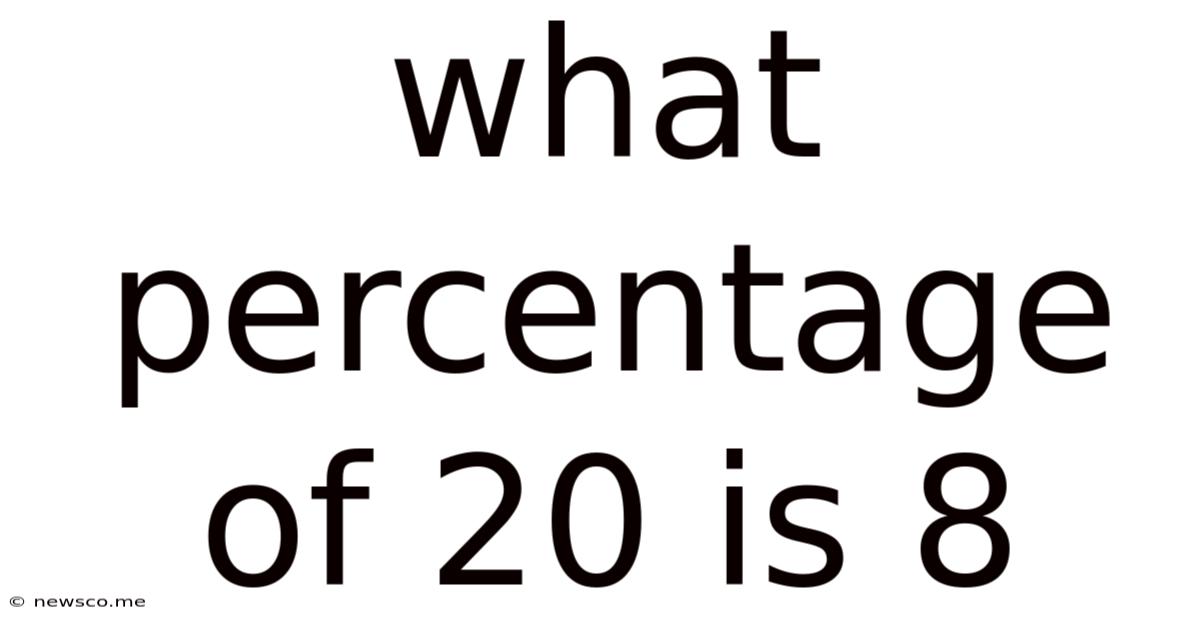
Table of Contents
What Percentage of 20 is 8? A Comprehensive Guide to Percentage Calculations
This seemingly simple question, "What percentage of 20 is 8?", opens the door to a world of practical applications for percentages in everyday life. Understanding how to calculate percentages is crucial for various aspects of life, from budgeting and shopping to understanding financial reports and analyzing data. This comprehensive guide will not only answer the question directly but also explore the underlying concepts, provide multiple methods for solving percentage problems, and offer real-world examples to solidify your understanding.
Understanding Percentages: The Basics
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" signifies "percent," meaning "out of 100." Therefore, 50% means 50 out of 100, which is equivalent to ½ or 0.5 as a decimal.
Understanding this fundamental concept is crucial for tackling any percentage problem, including the question at hand: What percentage of 20 is 8?
Method 1: The Proportion Method
This method uses the concept of setting up a proportion. A proportion is a statement that two ratios are equal. We can express the problem as a ratio:
- 8 is to 20 as x is to 100
This translates to the following equation:
8/20 = x/100
To solve for x (the percentage), we can cross-multiply:
20x = 800
Now, divide both sides by 20:
x = 40
Therefore, 8 is 40% of 20.
Method 2: The Decimal Method
This method involves converting the fraction into a decimal and then multiplying by 100 to express it as a percentage.
-
Form the fraction: Represent the problem as a fraction: 8/20
-
Convert to decimal: Divide the numerator (8) by the denominator (20): 8 ÷ 20 = 0.4
-
Convert to percentage: Multiply the decimal by 100: 0.4 x 100 = 40%
Again, we arrive at the answer: 8 is 40% of 20.
Method 3: Using a Calculator
Most calculators have a percentage function. You can input the problem directly:
(8 ÷ 20) x 100 = 40%
This is the quickest method, especially for more complex percentage calculations.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios. Here are a few examples:
1. Discounts and Sales
Retail stores frequently offer discounts expressed as percentages. For instance, a 20% discount on a $100 item means you save $20 (20% of $100). Calculating the final price requires understanding percentage reductions.
2. Taxes and Interest
Taxes and interest rates are commonly expressed as percentages. Calculating the tax amount or the total amount with interest involves using percentage calculations. For example, a 7% sales tax on a $50 purchase means a tax of $3.50.
3. Financial Statements
Understanding financial statements like income statements and balance sheets requires proficiency in percentage calculations. Analyzing profit margins, return on investment (ROI), and other key financial metrics relies on percentage comparisons.
4. Grade Calculations
In education, grades are often expressed as percentages. Calculating your overall grade in a course involves averaging percentages from different assignments and exams.
5. Data Analysis
In various fields, data is analyzed using percentages to represent proportions and trends. For instance, market share, survey results, and statistical data are frequently presented using percentages.
6. Tip Calculations
When dining out, it's customary to leave a tip, typically expressed as a percentage of the bill. Quickly calculating a 15% or 20% tip involves knowing how to calculate percentages efficiently.
Beyond the Basics: Solving More Complex Percentage Problems
While "What percentage of 20 is 8?" is a straightforward problem, let's explore more complex scenarios that build upon the fundamental principles we've learned:
Scenario 1: Finding the Percentage Increase or Decrease
Suppose a product's price increased from $50 to $60. What is the percentage increase?
-
Find the difference: $60 - $50 = $10
-
Divide the difference by the original price: $10 / $50 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 x 100 = 20%
Therefore, the price increased by 20%.
Scenario 2: Finding the Original Value
If a discounted item costs $40 after a 25% discount, what was the original price?
Let 'x' be the original price. The discounted price is 75% (100% - 25%) of the original price.
0.75x = $40
x = $40 / 0.75 = $53.33 (approximately)
The original price was approximately $53.33.
Scenario 3: Finding a Percentage of a Percentage
What is 15% of 20% of 100?
First, find 20% of 100: 0.20 x 100 = 20
Then, find 15% of 20: 0.15 x 20 = 3
Therefore, 15% of 20% of 100 is 3.
Practical Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more confident and efficient you'll become.
- Use different methods: Experiment with the proportion, decimal, and calculator methods to find the approach that best suits your understanding and the problem's complexity.
- Break down complex problems: Divide complex percentage problems into smaller, manageable steps.
- Check your work: Always double-check your calculations to ensure accuracy.
- Use online resources: Many online resources and calculators can help you practice and verify your answers.
Conclusion: Percentages in Our Daily Lives
The seemingly simple question, "What percentage of 20 is 8?", has led us on a journey through the world of percentage calculations. We've not only answered the initial question (40%) but also explored various methods for solving percentage problems and highlighted their practical applications in numerous real-world scenarios. Mastering percentage calculations empowers you to navigate various aspects of life more confidently and effectively, from managing finances to interpreting data and making informed decisions. By understanding and applying the concepts discussed, you can confidently tackle any percentage-related challenge you encounter.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 20 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.