What Percentage Of 80 Is 100
News Co
Apr 14, 2025 · 5 min read
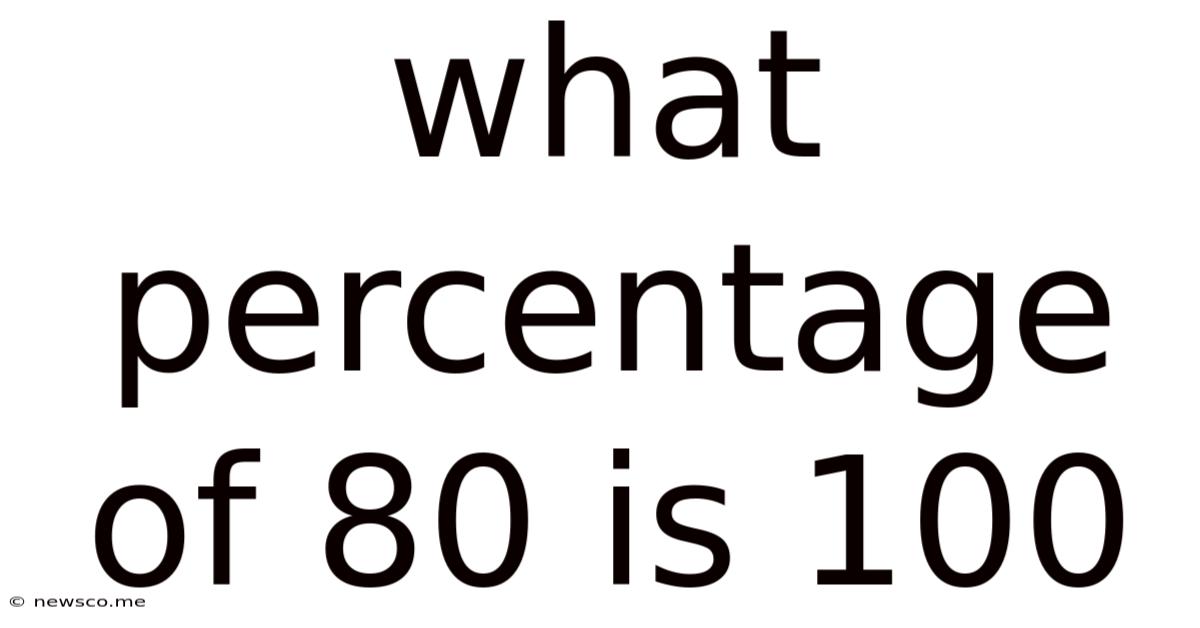
Table of Contents
What Percentage of 80 is 100? Understanding Percentage Calculations
This seemingly simple question – "What percentage of 80 is 100?" – delves into the core concepts of percentage calculations. While it might seem counterintuitive that a smaller number (80) could contain a larger number (100) as a percentage, understanding the underlying mathematical principles reveals a clear and straightforward solution. This article will not only provide the answer but also explore the various methods of solving percentage problems, providing you with the tools to tackle similar calculations confidently.
Understanding Percentages: The Basics
Before diving into the problem, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Percentage problems often involve three key components:
- The Part: This represents the portion of the whole we're interested in.
- The Whole: This is the total amount or the entire quantity.
- The Percentage: This expresses the relationship between the part and the whole as a fraction of 100.
Method 1: Setting up a Proportion
One of the most common methods for solving percentage problems is by setting up a proportion. A proportion is an equation that states that two ratios are equal. In this case, we can set up the proportion as follows:
Part / Whole = Percentage / 100
In our problem, the "part" is 100, and the "whole" is 80. Let's represent the unknown percentage as "x":
100 / 80 = x / 100
To solve for x, we can cross-multiply:
100 * 100 = 80 * x
10000 = 80x
Now, divide both sides by 80:
x = 10000 / 80
x = 125
Therefore, 100 is 125% of 80.
Method 2: Using Decimal Conversion
Another approach involves converting the percentage to a decimal and then solving the equation. We can set up the equation as follows:
Part = Percentage * Whole
In this case, we know the part (100) and the whole (80), but we need to find the percentage (let's call it 'x'). First, we can convert 'x' to a decimal by dividing it by 100: x/100
The equation then becomes:
100 = (x/100) * 80
Now, solve for x:
10000 = 80x
x = 10000 / 80
x = 125
Again, this confirms that 100 is 125% of 80.
Method 3: Understanding the Concept of "More Than 100%"
The result of 125% might seem unusual at first glance. It's crucial to understand that percentages can be greater than 100%. This simply means that the "part" is larger than the "whole." In this case, 100 is larger than 80, indicating a percentage exceeding 100%. Think of it like this: if you increase 80 by 25%, you get 100 (80 * 0.25 = 20; 80 + 20 = 100). Therefore, 100 represents 125% of the original 80.
Real-World Applications of Percentage Calculations Over 100%
While seemingly abstract, calculating percentages greater than 100% has numerous practical applications in various fields:
1. Business and Finance:
- Growth and Increase: Companies often use percentages over 100% to demonstrate significant growth in sales, profits, or market share compared to previous periods. For example, a company might report a 150% increase in revenue year-over-year.
- Return on Investment (ROI): Investors use percentages to calculate the ROI of their investments. If an investment of $80 yields a return of $100, the ROI is 125%.
- Inflation: Inflation rates exceeding 100% indicate hyperinflation, a severe economic condition where the value of currency declines dramatically.
2. Science and Engineering:
- Data Analysis: In scientific research, percentages over 100% might arise when comparing experimental results to control groups or comparing measurements over time. For example, a 120% increase in the size of a cell culture might be observed.
- Engineering Design: Engineers might use percentages over 100% when scaling up designs or comparing performance metrics.
3. Everyday Life:
- Recipe Scaling: If you need to double a recipe, you're essentially increasing the ingredients by 100%. Similarly, increasing a recipe by 50% means multiplying the quantities by 150%.
- Sales and Discounts: While less common, there are scenarios where the price of something increases by a percentage that would calculate above 100% of the original price. Consider a situation where a limited edition collectible goes from a price of $80 to a resale price of $100. This could be interpreted as 125% of the original price.
Beyond the Basics: Advanced Percentage Calculations
Understanding the core concepts of percentages allows you to tackle more complex scenarios. For instance:
- Calculating Percentage Change: The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100. This formula is crucial for analyzing changes in various data points. - Calculating Percentage Increase or Decrease: These calculations are very common in business, finance, and many other fields. To calculate a percentage increase, add the increase to the original amount. To calculate a percentage decrease, subtract the decrease from the original amount.
- Finding the Original Value: This is a reverse percentage calculation. For example, if you have a value that is a certain percentage of an unknown original, you can find the original value by dividing the current value by the decimal equivalent of the percentage.
Conclusion: Mastering Percentage Calculations
The question "What percentage of 80 is 100?" provides a valuable opportunity to solidify your understanding of percentage calculations, particularly those involving values exceeding 100%. By mastering the various methods discussed – setting up proportions, using decimal conversions, and understanding the concept of percentages over 100% – you'll gain the confidence to tackle a wide range of percentage problems, empowering you to navigate various aspects of life, business, and academic pursuits. Remember to always carefully define your "part" and your "whole" and choose the method best suited to the specific problem you are attempting to solve. The key is practice and application. The more you engage with percentage calculations, the more proficient you will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percentage Of 80 Is 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.