What The Square Root Of 400
News Co
Apr 06, 2025 · 6 min read
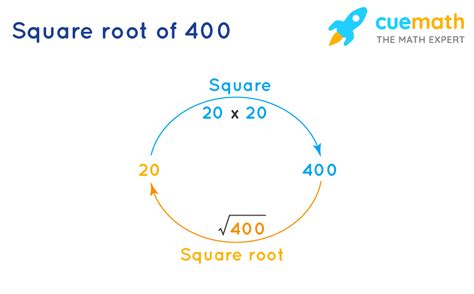
Table of Contents
What is the Square Root of 400? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What is the square root of 400?" opens a door to a fascinating world of mathematics, encompassing fundamental concepts and practical applications across various fields. This comprehensive guide will not only answer that question but also explore the broader implications of square roots, their properties, and their relevance in everyday life and advanced studies.
Understanding Square Roots: The Basics
Before diving into the specific case of the square root of 400, let's establish a firm understanding of what a square root actually is. In essence, the square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This is often represented mathematically as √9 = 3.
The symbol '√' is the radical symbol, indicating the square root operation. Numbers that have whole number square roots are known as perfect squares (e.g., 1, 4, 9, 16, 25, etc.).
Calculating the Square Root of 400
Now, let's address the central question: What is the square root of 400? The answer is 20. This is because 20 x 20 = 400. Therefore, √400 = 20.
However, it's important to note that every positive number has two square roots: a positive and a negative. While √400 = 20, it's also true that (-20) x (-20) = 400. Therefore, a complete answer would be ±20 (plus or minus 20). In many practical applications, the positive square root is the one primarily used, but understanding the existence of both is crucial for a comprehensive grasp of the concept.
Methods for Calculating Square Roots
While the square root of 400 is relatively straightforward, calculating the square root of other numbers might require different approaches. Here are some common methods:
1. Prime Factorization
This method is particularly useful for perfect squares. We break down the number into its prime factors. For 400:
400 = 2 x 2 x 2 x 2 x 5 x 5 = 2⁴ x 5²
Since square roots involve finding pairs of factors, we can see that we have two pairs of 2s and one pair of 5s. Therefore, the square root is 2 x 2 x 5 = 20.
2. Using a Calculator
For larger or non-perfect squares, a calculator is often the most efficient tool. Most calculators have a dedicated square root function (√). Simply input the number and press the square root button.
3. The Babylonian Method (or Heron's Method)
This is an iterative method that provides increasingly accurate approximations of square roots. It involves repeatedly refining an initial guess using the formula:
xₙ₊₁ = ½ (xₙ + a/xₙ)
where:
- xₙ is the current guess
- a is the number whose square root is being calculated
- xₙ₊₁ is the next, improved guess
This method is particularly useful for approximating square roots without a calculator.
4. Long Division Method
Similar to the Babylonian method, the long division method is a manual process for approximating square roots. It's a more complex method and less commonly used today due to the availability of calculators.
Applications of Square Roots in Various Fields
The concept of square roots extends far beyond simple mathematical exercises. It finds practical application in numerous fields, including:
1. Geometry and Trigonometry
Square roots are fundamental in geometry, particularly when calculating distances, areas, and volumes. For instance, the Pythagorean theorem (a² + b² = c²) relies heavily on square roots to find the length of the hypotenuse of a right-angled triangle. In trigonometry, the concept of square roots is integral to calculating various trigonometric functions and solving geometric problems. Finding the diagonal of a square or rectangle uses the application of the Pythagorean Theorem, thus leveraging the concept of square root.
2. Physics and Engineering
In physics and engineering, square roots are used extensively in calculations related to motion, energy, and forces. For example, calculating velocity, acceleration, and kinetic energy often involve the use of square roots. These calculations can be seen in applications across multiple engineering disciplines, like electrical and mechanical engineering. Understanding the effect of various forces and energies relies on accurately applying square roots.
3. Statistics and Data Analysis
Square roots play a crucial role in statistical analysis, particularly in calculating standard deviation and variance. These measures help quantify the spread or dispersion of a data set, providing crucial insights into the nature of the data being analyzed. Moreover, many statistical tests use square roots as a fundamental component in their calculations.
4. Computer Graphics and Game Development
In computer graphics and game development, square roots are used extensively for distance calculations, vector normalization, and other geometrical computations. These calculations are critical for rendering 3D environments, simulating movement and collision detection, and creating realistic game physics.
5. Finance and Investment
Square roots are also employed in financial calculations, such as determining the standard deviation of investment returns or calculating portfolio variance. These calculations are crucial for risk management and investment strategies.
Advanced Concepts Related to Square Roots
Beyond the basic understanding of square roots, there are several more advanced concepts worth exploring:
1. Complex Numbers
When dealing with negative numbers under the square root symbol, we enter the realm of imaginary numbers. The square root of a negative number is defined as an imaginary number. For instance, √(-1) = i, where 'i' is the imaginary unit. Combining real and imaginary numbers leads to the concept of complex numbers, which have applications in various areas, including electrical engineering and quantum mechanics.
2. nth Roots
The square root is a specific case of the nth root, where n=2. The nth root of a number 'a' is a value that, when raised to the power of 'n', equals 'a'. For instance, the cube root (n=3) of 8 is 2 because 2³ = 8.
3. Irrational Numbers
Many numbers do not have exact square roots that can be expressed as a simple fraction. These are known as irrational numbers, such as the square root of 2 (√2) or the square root of 3 (√3). These numbers have non-repeating, non-terminating decimal expansions.
Conclusion: The Enduring Importance of Square Roots
The seemingly simple question of the square root of 400 has led us on a journey through fundamental mathematical concepts and their diverse applications. From basic calculations to advanced mathematical theories, the importance of square roots is undeniable across various scientific, engineering, and financial disciplines. Understanding square roots is not only essential for mathematical proficiency but also for navigating the complexities of the world around us. Whether you're solving a geometric problem, analyzing data, or developing a computer game, a firm grasp of this fundamental concept is invaluable.
Latest Posts
Latest Posts
-
33 As A Fraction In Simplest Form
Apr 09, 2025
-
A Rational Number That Is Not An Integer
Apr 09, 2025
-
Whats The Square Root Of 33
Apr 09, 2025
-
What Number Makes The Equation True
Apr 09, 2025
-
What Are The Factors For 81
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about What The Square Root Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.