What Two Numbers Multiply To 27
News Co
Apr 04, 2025 · 5 min read
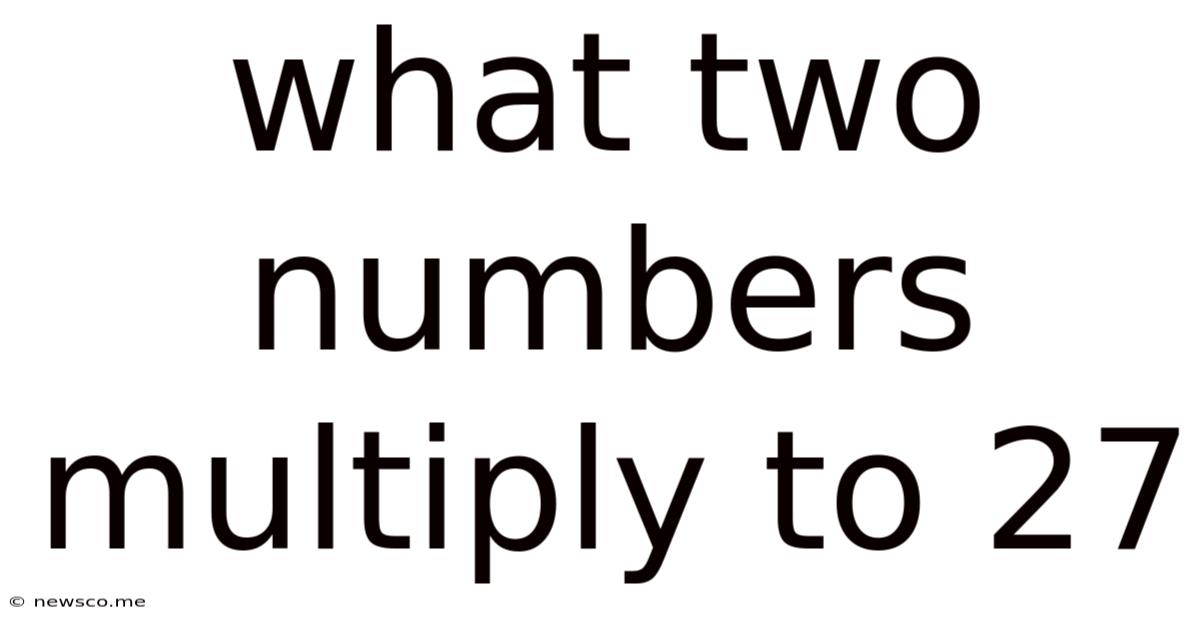
Table of Contents
What Two Numbers Multiply to 27? Exploring Factors and Prime Factorization
Finding two numbers that multiply to 27 might seem like a simple arithmetic problem, but it opens the door to understanding fundamental concepts in mathematics, particularly factorization and prime numbers. This exploration will delve into various approaches to solving this problem, demonstrating the versatility of mathematical thinking and its applications beyond simple multiplication.
Understanding Factors and Multiples
Before we dive into the specific solution, let's clarify the terms "factors" and "multiples." Factors are numbers that divide evenly into a given number without leaving a remainder. In other words, if you multiply two or more factors together, you get the original number. Multiples, on the other hand, are numbers obtained by multiplying a given number by any integer.
For example, let's consider the number 12. Its factors are 1, 2, 3, 4, 6, and 12. Multiples of 12 include 12, 24, 36, 48, and so on. Our problem focuses on finding the factors of 27.
Finding the Factors of 27: A Systematic Approach
The simplest way to find the factors of 27 is to systematically test numbers. We start with 1 and work our way up:
- 1 x 27 = 27: This is the most obvious pair. 1 is a factor of every number.
- 3 x 9 = 27: This is another factor pair.
Since 3 and 9 are factors, we don't need to continue testing numbers larger than 9, as they would not produce integer factors when multiplied by another number to equal 27. Therefore, the integer factor pairs of 27 are (1, 27) and (3, 9).
Prime Factorization: Unveiling the Building Blocks
Prime factorization is a powerful technique that breaks down a number into its prime factors – numbers that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). Understanding prime factorization helps us understand the fundamental building blocks of a number.
To find the prime factorization of 27:
- Start with the smallest prime number, 2. 27 is not divisible by 2.
- Move to the next prime number, 3. 27 is divisible by 3 (27 / 3 = 9).
- Continue the process. Now, we consider 9. It's also divisible by 3 (9 / 3 = 3).
- The final step. We've reached a prime number, 3.
Therefore, the prime factorization of 27 is 3 x 3 x 3, or 3³. This shows that 27 is composed entirely of the prime factor 3. This information is invaluable in many areas of mathematics, such as simplifying fractions and solving algebraic equations.
Beyond Integer Factors: Exploring Rational and Real Numbers
While we've focused on integer factors, it's important to note that we can extend the concept to include rational and real numbers. If we allow for fractions and decimals, we can find infinitely many pairs of numbers that multiply to 27.
For example:
- 2.7 x 10 = 27
- 13.5 x 2 = 27
- 0.5 x 54 = 27
And so on. The number of possibilities becomes infinite when considering rational and real numbers.
Applications of Factorization: Real-World Examples
The ability to find factors and perform prime factorization has far-reaching applications in various fields:
- Cryptography: Prime factorization is crucial in modern cryptography, especially in RSA encryption, which relies on the difficulty of factoring large numbers into their prime components to secure data transmission.
- Computer Science: Factorization algorithms are fundamental in computational number theory and play a vital role in optimizing various computer programs.
- Engineering: Factorization techniques are used in engineering design and analysis to simplify complex systems and improve efficiency.
- Everyday Math: Understanding factors is essential for simplifying fractions, finding common denominators, and solving many everyday mathematical problems.
Exploring Negative Factors
We've primarily discussed positive factors, but it's important to consider negative numbers as well. Since multiplying two negative numbers results in a positive number, we also have the factor pairs (-1, -27) and (-3, -9). Thus, the complete set of integer factor pairs for 27 includes both positive and negative combinations.
Expanding the Concept: More than Two Numbers
The question initially focused on two numbers, but we can broaden the perspective to include more than two numbers. For instance:
- 1 x 3 x 9 = 27
- 1 x 1 x 1 x 3 x 3 x 3 = 27 (using the prime factorization)
The Importance of Context: Problem Solving in Mathematics
The approach to solving "What two numbers multiply to 27?" depends heavily on the context. If the question is posed in an elementary school setting, the answer likely focuses on integer factors. In a more advanced mathematical context, the answer might involve rational, real, or even complex numbers, broadening the range of possible solutions significantly.
Mathematical Curiosity: Exploring Patterns and Relationships
By exploring this seemingly simple problem, we uncover deeper mathematical concepts and relationships. The prime factorization reveals the essential structure of the number 27, revealing its inherent properties and how it relates to other numbers. This exercise highlights the beauty and elegance of mathematics, showing how seemingly simple problems can lead to a deeper understanding of the subject.
Conclusion: Beyond the Answer
The answer to "What two numbers multiply to 27?" is not just (1, 27) and (3, 9). The real value lies in the journey of exploration, the understanding of factors, prime factorization, and the realization that mathematical concepts have far-reaching applications beyond the initial problem. This problem serves as a gateway to deeper mathematical understanding, demonstrating the interconnectedness and power of mathematical concepts. The process of finding the solution, more so than the solution itself, fosters critical thinking and problem-solving skills, crucial elements in mathematical literacy and beyond. The exploration continues; the numbers hold a multitude of stories waiting to be uncovered.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Two Numbers Multiply To 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.