What's 1 2 Of 1 4
News Co
Mar 18, 2025 · 5 min read
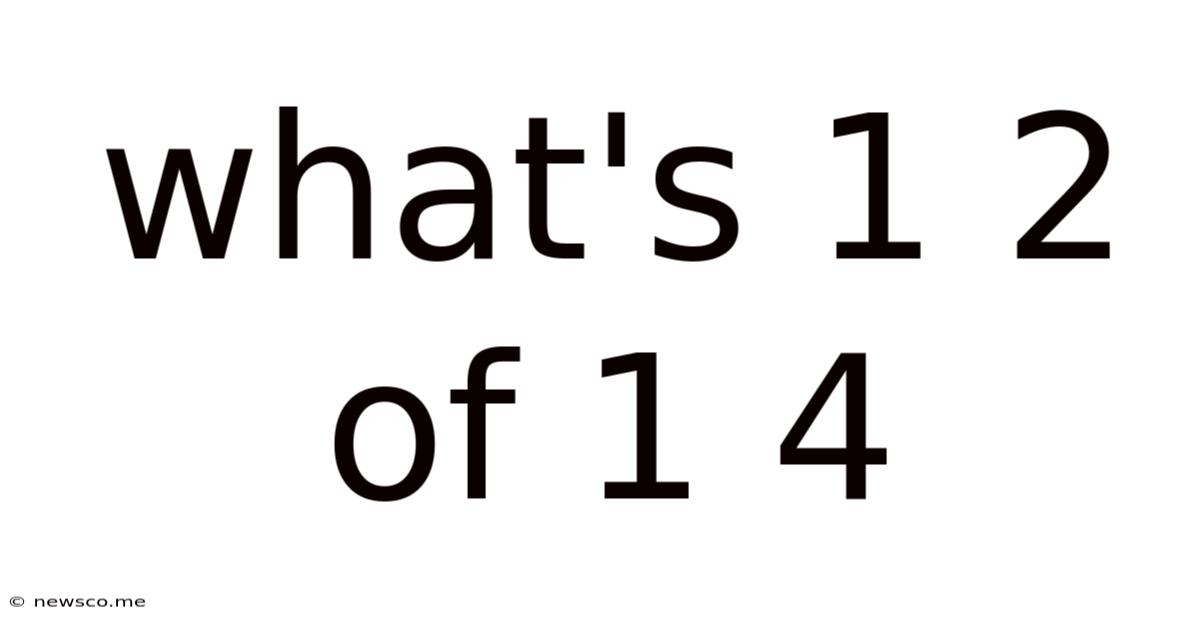
Table of Contents
What's 1/2 of 1/4? A Deep Dive into Fractions and Their Applications
Understanding fractions is fundamental to mathematics and numerous real-world applications. This article will thoroughly explore the question, "What's 1/2 of 1/4?", providing a step-by-step solution, delving into the underlying concepts, and showcasing various practical examples where this type of calculation is essential. We'll also explore different methods for solving this problem and discuss the broader implications of fractional arithmetic.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's solidify our understanding of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
For example, in the fraction 1/4, the numerator (1) indicates one part, while the denominator (4) means the whole is divided into four equal parts.
Calculating 1/2 of 1/4: The Step-by-Step Solution
To find 1/2 of 1/4, we perform multiplication. The word "of" in this context signifies multiplication. Therefore, the calculation is:
(1/2) x (1/4)
Multiplying fractions involves multiplying the numerators together and the denominators together:
(1 x 1) / (2 x 4) = 1/8
Therefore, 1/2 of 1/4 is 1/8.
Visualizing the Solution
Visual aids can greatly enhance understanding. Imagine a pizza cut into four equal slices. 1/4 represents one of these slices. Now, let's take half (1/2) of that single slice. We would effectively divide that slice into two equal parts, and each part would represent 1/8 of the whole pizza.
Alternative Methods for Solving the Problem
While the direct multiplication method is the most straightforward, let's explore alternative approaches:
Method 1: Converting to Decimals
We can convert the fractions to decimals before multiplying:
- 1/2 = 0.5
- 1/4 = 0.25
Then, multiply the decimal values:
0.5 x 0.25 = 0.125
Converting 0.125 back to a fraction gives us 1/8.
Method 2: Using a Diagram
A visual representation can be extremely helpful. Draw a rectangle and divide it into four equal parts. Shade one part to represent 1/4. Then, divide the shaded part into two equal parts. You'll see that each of these smaller parts represents 1/8 of the original rectangle.
Real-World Applications of Fractional Arithmetic
Fractional arithmetic isn't just a classroom exercise; it's a crucial skill applied across various fields:
1. Cooking and Baking:
Recipes frequently use fractions. If a recipe calls for 1/4 cup of sugar and you only want to make half the recipe, you'll need to calculate 1/2 of 1/4 cup, resulting in 1/8 cup of sugar.
2. Construction and Engineering:
Precise measurements are critical. Calculating the amount of materials needed for a project often involves fractions. For instance, determining the length of a beam that is 1/2 the length of a 1/4-mile track.
3. Finance:
Fractions are essential in financial calculations, such as determining interest rates, calculating portions of investments, or understanding stock prices.
4. Data Analysis:
Representing portions of data sets often involves fractions. For example, calculating the percentage of a population that falls within a specific demographic.
5. Science:
In scientific experiments, measurements frequently involve fractions. For example, precise dilutions in chemistry or determining the proportion of elements in a compound.
Expanding on the Concept: More Complex Fractional Calculations
The principles used to solve "1/2 of 1/4" can be applied to more complex fractional calculations. Let's explore some examples:
-
Finding a fraction of a fraction: For example, finding 2/3 of 3/5. This would be (2/3) x (3/5) = 6/15, which simplifies to 2/5.
-
Mixed numbers: Mixed numbers combine a whole number and a fraction (e.g., 1 1/2). To multiply with a mixed number, first convert it into an improper fraction. For example, 1 1/2 is equal to 3/2.
-
Dividing fractions: Dividing fractions involves inverting the second fraction and then multiplying. For example, 1/2 divided by 1/4 is equivalent to (1/2) x (4/1) = 4/2 = 2.
Mastering Fractions: Tips and Resources
Developing a strong understanding of fractions takes time and practice. Here are some helpful tips:
-
Practice regularly: Solve various problems involving fractions to build your skills.
-
Use visual aids: Diagrams and models can make understanding fractions easier.
-
Utilize online resources: Many websites and educational platforms offer interactive lessons and practice exercises.
-
Break down complex problems: Divide larger problems into smaller, more manageable steps.
-
Check your work: Always double-check your answers to ensure accuracy.
Conclusion: The Importance of Fractional Understanding
The seemingly simple question, "What's 1/2 of 1/4?", unveils a deeper understanding of fractions and their widespread applicability. Mastering fractional arithmetic is not merely an academic pursuit; it's a crucial life skill with practical implications across diverse fields. By understanding the fundamental principles and applying the various methods discussed, you'll be well-equipped to tackle complex fractional calculations with confidence. Remember to practice regularly, utilize visual aids, and explore various resources to strengthen your understanding of this essential mathematical concept. The ability to confidently and accurately work with fractions will undoubtedly enhance your problem-solving skills and open doors to a wider range of opportunities in your academic and professional pursuits.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's 1 2 Of 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.