What's 1 2 Of 3 4
News Co
Apr 23, 2025 · 5 min read
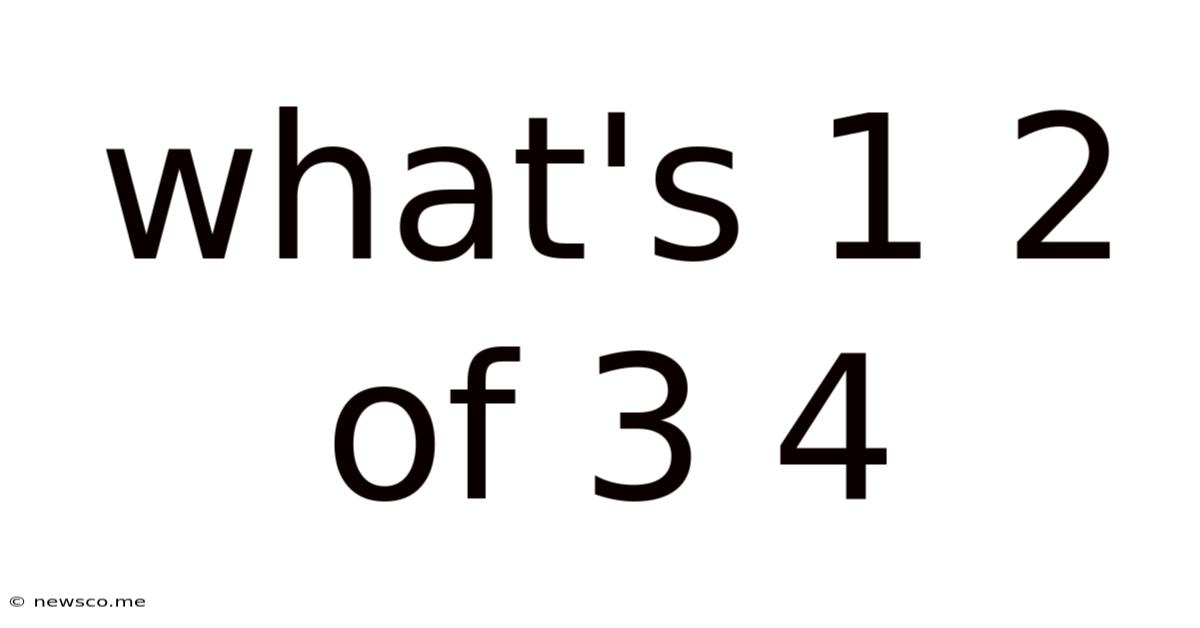
Table of Contents
What's 1 2 of 3 4? Unraveling the Enigma of Mathematical Ambiguity
The seemingly simple question, "What's 1 2 of 3 4?" is a deceptively complex problem that highlights the importance of clear mathematical notation and the potential for ambiguity in interpreting mathematical expressions. This seemingly straightforward query actually unveils a fascinating exploration into the order of operations, the crucial role of parentheses, and the different ways we can interpret and solve mathematical problems. Let's delve into the intricacies of this mathematical puzzle and explore the various solutions, emphasizing the importance of precise notation for avoiding confusion.
The Problem with Implicit Multiplication
The core issue lies in the lack of explicit operators. The expression "1 2 of 3 4" uses juxtaposition, placing numbers directly next to each other without clear operators like '+' (addition), '-' (subtraction), '×' (multiplication), or '÷' (division). This ambiguity is the source of multiple possible interpretations. Without parentheses or explicitly stated operations, the order of operations (PEMDAS/BODMAS) becomes difficult to apply definitively. Let's analyze the potential interpretations:
Interpretation 1: Sequential Multiplication
One interpretation treats the expression as a sequence of multiplications. We can read it as (1 × 2) × (3 × 4). This approach is straightforward:
- 1 × 2 = 2
- 3 × 4 = 12
- 2 × 12 = 24
Therefore, under this interpretation, the answer is 24. This is a perfectly valid interpretation if we assume the spaces represent implied multiplication.
Interpretation 2: Fractional Interpretation
Another approach involves interpreting "of" as multiplication and structuring the expression as a fraction. We can consider it as (1/2) multiplied by (3/4). This is a common interpretation when dealing with phrases like "one-half of".
- 1/2 × 3/4 = 3/8
Therefore, under this fractional interpretation, the answer is 3/8 or 0.375. This interpretation relies on a specific understanding of the word "of" within a mathematical context.
Interpretation 3: Mixed Operations and Grouping
We could also interpret the expression as a combination of operations, potentially implying different groupings. Without clear parentheses, we're free to explore various combinations. For example:
- (1 + 2) × (3 + 4) = 21: This interpretation sums the numbers within implicit groupings before multiplying.
- (1 × 2) + (3 × 4) = 14: This prioritizes multiplication before addition.
- 1 + (2 × 3) + 4 = 11: This approach involves prioritizing multiplication within a specific order.
These interpretations demonstrate that the absence of explicit operators and parentheses leads to a wide range of potential numerical results.
The Crucial Role of Parentheses
The inconsistencies above highlight the vital importance of parentheses in mathematical notation. Parentheses (or brackets) serve to clarify the order of operations and remove ambiguity. Let's see how different parenthetical structures affect the outcome:
- (1 × 2) × (3 × 4) = 24: This is unambiguous and produces the same result as Interpretation 1.
- (1/2) × (3 × 4) = 6: This interprets "of" as multiplication but alters the order.
- 1 × (2 × (3 × 4)) = 24: This shows a different grouping which still yields the same result as the first example.
- ((1 + 2) × 3) × 4 = 36: This exemplifies how parentheses influence the result and alter the meaning of the expression.
The examples above demonstrate how strategically placing parentheses dramatically alters the outcome. The addition of parentheses provides a clear structure, ensuring that the expression is understood and calculated consistently.
The Significance of Mathematical Precision
The ambiguity of "1 2 of 3 4" is a compelling illustration of why clear mathematical notation is essential. In any field relying on mathematics – from engineering and physics to finance and computer science – ambiguity can lead to significant errors and incorrect results. The simple omission of an operator or the absence of parentheses can have catastrophic consequences, particularly in complex calculations or when dealing with sensitive data.
The problem extends beyond simple arithmetic. In more advanced mathematics, the importance of precise notation is amplified. Mathematical expressions often involve multiple variables, functions, and operations, demanding meticulous precision to avoid misunderstandings and ensure accurate results.
This simple arithmetic puzzle underscores the broader need for:
- Explicit Operators: Always use explicit multiplication, division, addition, and subtraction symbols to eliminate any possibility of misinterpretation.
- Strategic Use of Parentheses: Parentheses are crucial for controlling the order of operations and ensuring clarity. They act as unambiguous instruction guides for the calculations.
- Careful Writing: Always write mathematical expressions in a clear and unambiguous way, considering the potential for different interpretations.
Expanding the Context: Beyond Basic Arithmetic
While this problem involves basic arithmetic, the implications stretch into more complex mathematical contexts. Consider programming: programming languages utilize strict rules regarding order of operations and necessitate explicit operators and parentheses. Failure to follow these rules can lead to program crashes or incorrect outputs. The lessons learned from this simple expression are crucial when working with more intricate mathematical models and algorithms.
Similarly, in scientific notation, the lack of clarity can have severe consequences. In formulas and equations, proper use of parentheses and operators is paramount for correct calculations.
Conclusion: The Value of Clarity
The seemingly trivial question, "What's 1 2 of 3 4?" serves as a potent reminder of the importance of clear and unambiguous mathematical notation. The multiple interpretations arising from the lack of explicit operators and parentheses highlight the potential for miscommunication and error. By understanding the crucial roles of parentheses and explicit symbols, we can avoid ambiguity and ensure the consistent and accurate interpretation and calculation of mathematical expressions, irrespective of their complexity. The emphasis on clarity and precision is not merely a matter of mathematical correctness; it's a foundational element of reliable mathematical communication and problem-solving. This simple problem offers a valuable lesson in precision and the power of unambiguous notation across various fields that depend on mathematical accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's 1 2 Of 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.