What's 1 3 Plus 1 3
News Co
Mar 15, 2025 · 5 min read
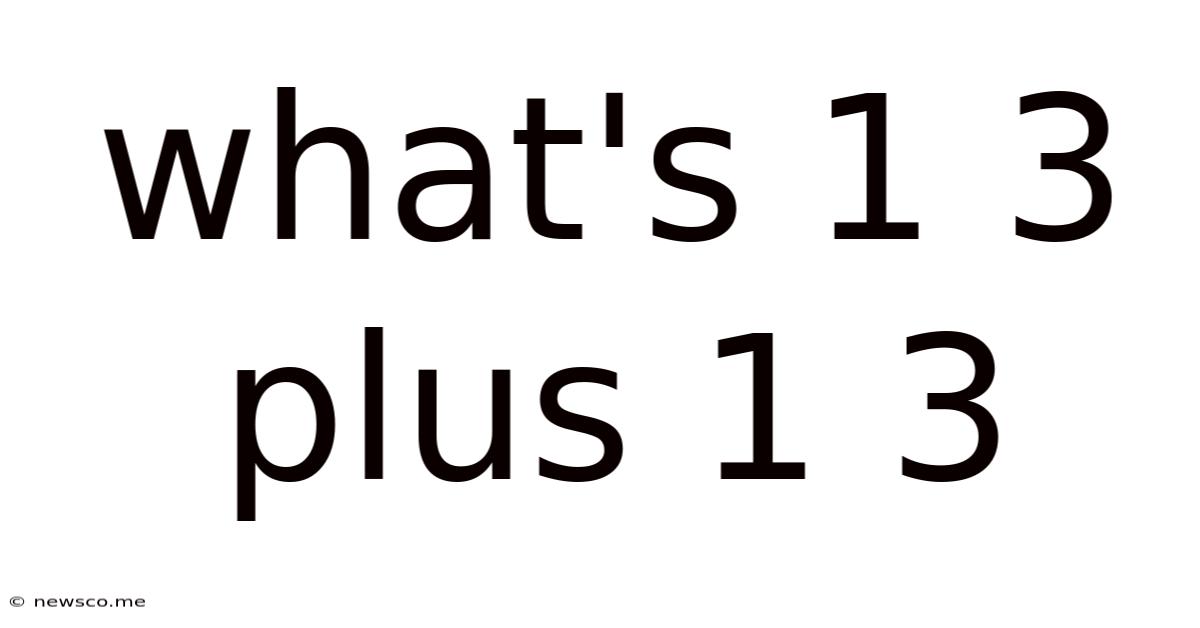
Table of Contents
What's 1/3 Plus 1/3? A Deep Dive into Fractions and Their Applications
The seemingly simple question, "What's 1/3 plus 1/3?" might appear trivial at first glance. However, understanding this basic addition problem forms the bedrock for grasping more complex mathematical concepts, particularly within the realm of fractions. This article delves into the solution, exploring the underlying principles of fraction addition and showcasing the broad applicability of fractions across various fields.
Understanding Fractions: A Foundation for Addition
Before tackling the addition problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two essential components:
- Numerator: The top number indicates how many parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
In the fraction 1/3, the numerator (1) signifies that we have one part, while the denominator (3) indicates that the whole is divided into three equal parts. Visualizing this with a pie cut into three slices helps clarify the concept. One slice represents 1/3 of the whole pie.
Adding Fractions with Common Denominators
Adding fractions becomes straightforward when they share the same denominator. This is the case with our problem: 1/3 + 1/3. Since both fractions have a denominator of 3, we can simply add the numerators while keeping the denominator unchanged:
1/3 + 1/3 = (1 + 1) / 3 = 2/3
Therefore, 1/3 plus 1/3 equals 2/3.
This simple addition demonstrates a crucial rule: when adding fractions with the same denominator, add the numerators and retain the common denominator.
Visualizing the Addition: The Power of Representation
Visual aids can significantly enhance understanding, especially when dealing with abstract concepts like fractions. Imagine two pies, each cut into three equal slices. If we take one slice from the first pie (1/3) and one slice from the second pie (1/3), we now possess two slices out of a possible six (if we combine both pies). This visually represents 2/3. This approach helps solidify the concept of fraction addition for beginners.
Extending the Concept: Adding Fractions with Different Denominators
The scenario becomes slightly more complex when adding fractions with unlike denominators. For instance, let's consider 1/3 + 1/2. In this case, we must find a common denominator—a number divisible by both 3 and 2. The least common multiple (LCM) of 3 and 2 is 6.
To convert 1/3 to have a denominator of 6, we multiply both the numerator and the denominator by 2: (1 * 2) / (3 * 2) = 2/6.
Similarly, to convert 1/2 to have a denominator of 6, we multiply both the numerator and the denominator by 3: (1 * 3) / (2 * 3) = 3/6.
Now, we can add the fractions: 2/6 + 3/6 = (2 + 3) / 6 = 5/6. Therefore, 1/3 + 1/2 = 5/6.
This illustrates the general rule: to add fractions with different denominators, find a common denominator, convert the fractions to equivalent fractions with the common denominator, and then add the numerators.
Real-World Applications of Fraction Addition
Fractions aren't confined to the abstract realm of mathematics; they permeate our everyday lives. Understanding fraction addition is crucial in numerous contexts:
Cooking and Baking:
Recipes often involve fractional measurements. Adding ingredients requires proficiency in fraction addition. For example, a recipe might call for 1/4 cup of sugar and 1/2 cup of flour. To determine the total amount of dry ingredients, we need to add these fractions.
Measurement and Construction:
Construction projects rely heavily on precise measurements. Adding fractional lengths of materials like wood or pipe is a common task requiring an understanding of fraction addition.
Finance and Budgeting:
Managing personal finances involves dealing with fractions of money. Calculating percentages, discounts, or portions of a budget requires understanding fraction addition. For example, you might spend 1/3 of your salary on rent and 1/4 on groceries. Adding these fractions helps understand your total expenditure.
Time Management:
Dividing your time efficiently often requires working with fractions of an hour or day. Scheduling tasks and allotting time to different activities demands competency in fraction addition.
Data Analysis and Statistics:
Fractions and their manipulation are essential in analyzing data and interpreting statistics. Understanding proportions and representing data using fractions is fundamental in many fields.
Beyond the Basics: Further Exploration of Fractions
The simple addition of 1/3 + 1/3 provides a gateway to more complex concepts within the world of fractions:
- Subtracting fractions: The principles of adding fractions directly translate to subtracting them. The same rules regarding common denominators apply.
- Multiplying fractions: Multiplying fractions involves multiplying the numerators and the denominators separately.
- Dividing fractions: Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
- Mixed numbers: These combine whole numbers and fractions (e.g., 2 1/2). Adding mixed numbers often requires converting them to improper fractions before performing addition.
- Decimal representation: Fractions can be expressed as decimals and vice versa. This connection broadens the applicability of fractions to various numerical representations.
Conclusion: The Importance of Mastering Fractions
The answer to "What's 1/3 plus 1/3?" is a seemingly simple 2/3. However, the underlying principles and applications of this basic fraction addition are far-reaching and profoundly significant. Mastering fraction addition is not merely about solving mathematical problems; it's about developing a fundamental understanding that has widespread applications in various real-world scenarios. From baking a cake to analyzing complex datasets, the ability to work confidently with fractions is an invaluable skill. This article aimed to provide a solid foundation for understanding fraction addition and its importance, encouraging further exploration of this crucial mathematical concept. Through practice and understanding, you can confidently tackle more challenging fraction problems and expand your mathematical capabilities.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about What's 1 3 Plus 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.