Whats 10 To The Power Of 4
News Co
Apr 20, 2025 · 5 min read
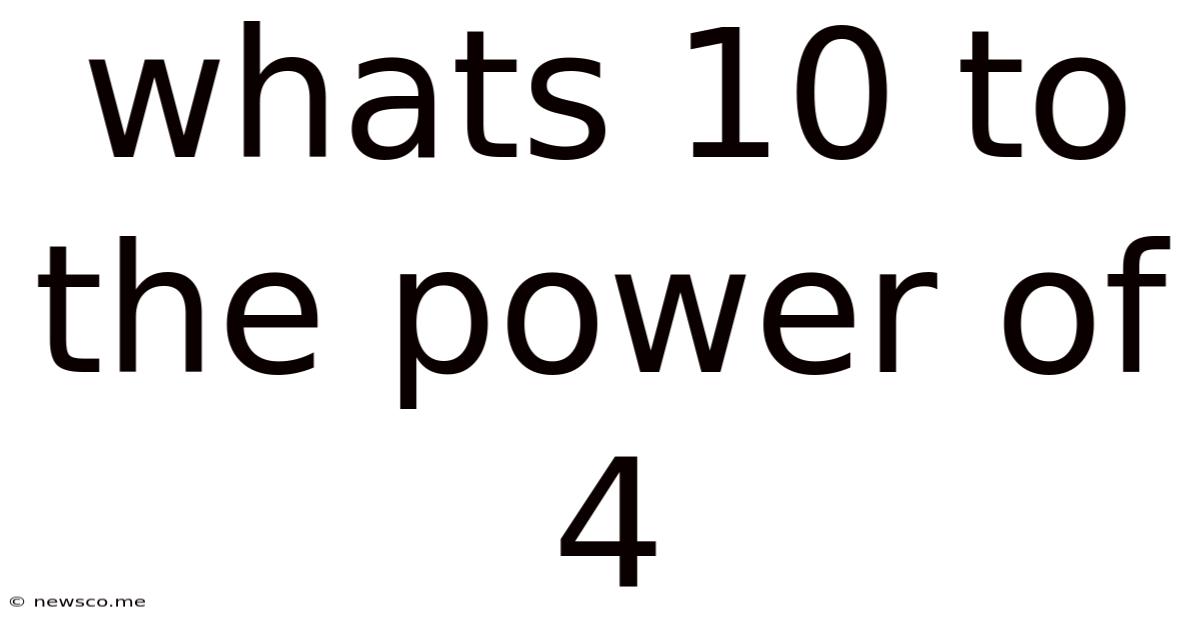
Table of Contents
What's 10 to the Power of 4? Unveiling the Fundamentals of Exponents
Understanding exponents is fundamental to mathematics and numerous scientific fields. This comprehensive guide delves into the seemingly simple question: "What's 10 to the power of 4?" We'll not only answer this directly but also explore the broader concepts of exponents, their applications, and how to solve similar problems efficiently. Prepare to unlock a deeper understanding of this core mathematical principle.
Deconstructing 10 to the Power of 4 (10⁴)
The expression "10 to the power of 4," written as 10⁴, represents repeated multiplication. It means multiplying the base number (10) by itself four times:
10⁴ = 10 × 10 × 10 × 10
Performing this calculation, we find:
10 × 10 = 100 100 × 10 = 1000 1000 × 10 = 10000
Therefore, 10 to the power of 4 equals 10,000.
Understanding Exponents: A Deeper Dive
Exponents, also known as powers or indices, are a concise way to represent repeated multiplication. A general exponent is written as bⁿ, where:
- b is the base: the number being multiplied.
- n is the exponent: the number of times the base is multiplied by itself.
For example, in 5³, 5 is the base, and 3 is the exponent. This means 5 × 5 × 5 = 125.
Key Properties of Exponents
Several properties govern how we work with exponents. Understanding these is crucial for solving more complex problems:
- Product of Powers: When multiplying two numbers with the same base, add the exponents: bᵐ × bⁿ = b⁽ᵐ⁺ⁿ⁾. For example, 2² × 2³ = 2⁵ = 32.
- Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: bᵐ ÷ bⁿ = b⁽ᵐ⁻ⁿ⁾. For example, 3⁵ ÷ 3² = 3³ = 27.
- Power of a Power: When raising a power to another power, multiply the exponents: (bᵐ)ⁿ = b⁽ᵐⁿ⁾. For example, (4²)³ = 4⁶ = 4096.
- Power of a Product: When raising a product to a power, raise each factor to that power: (ab)ⁿ = aⁿbⁿ. For example, (2 × 3)² = 2² × 3² = 4 × 9 = 36.
- Power of a Quotient: When raising a quotient to a power, raise both the numerator and the denominator to that power: (a/b)ⁿ = aⁿ/bⁿ (assuming b ≠ 0). For example, (2/3)² = 2²/3² = 4/9.
Applications of Exponents: Beyond the Basics
Exponents are not just a theoretical concept; they have widespread practical applications in various fields:
1. Scientific Notation: Expressing Very Large or Very Small Numbers
Scientific notation uses exponents to express extremely large or small numbers concisely. For instance, the speed of light is approximately 3 × 10⁸ meters per second. This is much easier to write and understand than 300,000,000.
2. Compound Interest Calculations: Growing Your Money
Understanding exponents is crucial for calculating compound interest. The formula involves exponents to determine the future value of an investment based on the principal amount, interest rate, and time period.
3. Computer Science: Data Storage and Processing
Computers use binary (base-2) systems, and exponents are essential in representing and manipulating data in memory and storage. Understanding how exponents work in binary is vital for computer programmers and data scientists.
4. Physics and Engineering: Modeling Natural Phenomena
Exponents frequently appear in physics and engineering formulas, describing phenomena like radioactive decay, wave propagation, and the behavior of circuits.
5. Biology: Population Growth and Decay
Exponential growth and decay models are essential in biology, used to describe population dynamics, bacterial growth, and the decay of radioactive isotopes used in medical imaging.
Solving Problems Involving Exponents: Practical Examples
Let's solidify our understanding with some examples:
Example 1: What is 5 to the power of 3 (5³)?
5³ = 5 × 5 × 5 = 125
Example 2: Simplify the expression 2⁵ × 2².
Using the product of powers rule, we add the exponents: 2⁵ × 2² = 2⁽⁵⁺²⁾ = 2⁷ = 128
Example 3: Simplify (3⁴)²
Using the power of a power rule, we multiply the exponents: (3⁴)² = 3⁽⁴ˣ²⁾ = 3⁸ = 6561
Example 4: Calculate the value of 10⁰
Any non-zero number raised to the power of 0 equals 1. Therefore, 10⁰ = 1. This is a crucial rule to remember.
Example 5: What is 10 to the power of -2 (10⁻²)?
Negative exponents represent reciprocals. 10⁻² = 1/10² = 1/100 = 0.01
Expanding on the Concept of 10⁴ and its Significance
Returning to our initial question, 10⁴ = 10,000. The significance of this number extends beyond a simple calculation. It forms the basis for understanding larger powers of 10, which are essential in scientific notation and representing large quantities. Understanding this base allows for easier comprehension of numbers like 10⁵ (100,000), 10⁶ (1,000,000), and so on. This establishes a foundational understanding of numerical scales that are vital in many scientific and engineering fields.
Mastering Exponents: Tips and Resources
Mastering exponents requires practice and a solid grasp of the fundamental rules. Here are some tips to improve your understanding:
- Practice Regularly: Work through numerous examples and problems to build your confidence and proficiency.
- Use Online Calculators: While calculators can provide answers, focus on understanding the underlying principles and using the calculator strategically to verify your solutions.
- Visual Aids: Diagrams and visual representations can aid in grasping the concept of repeated multiplication.
- Seek Help When Needed: Don't hesitate to ask for help from teachers, tutors, or online communities if you encounter difficulties.
By understanding the principles of exponents and practicing regularly, you'll be able to confidently tackle more complex mathematical problems and apply this essential skill across various fields. The seemingly simple question "What's 10 to the power of 4?" opens the door to a vast world of mathematical concepts and their real-world applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 10 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.