Whats 12/5 As A Mixed Number
News Co
Mar 25, 2025 · 5 min read
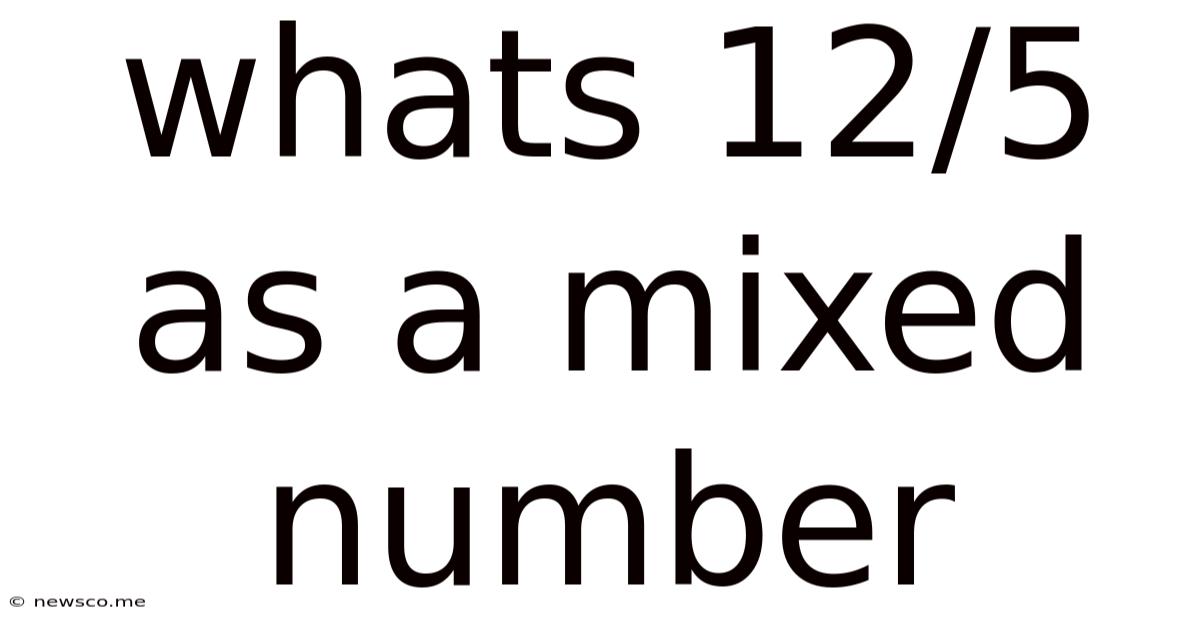
Table of Contents
What's 12/5 as a Mixed Number? A Comprehensive Guide
Converting improper fractions to mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 12/5 to a mixed number but will also delve into the underlying concepts, provide multiple methods for solving similar problems, and offer valuable tips and tricks to master this essential mathematical operation. We'll explore different approaches, explain the reasoning behind each step, and tackle common misconceptions. By the end, you'll be able to confidently convert any improper fraction to a mixed number with ease.
Understanding Improper Fractions and Mixed Numbers
Before we tackle the conversion of 12/5, let's clarify the terms involved:
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 12/5, and 5/5.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than its denominator (e.g., 1/2, 3/4, 2/5). Examples of mixed numbers include 1 1/2, 2 3/4, and 5 1/3.
The core idea behind converting an improper fraction to a mixed number is to represent the same quantity in a different, often more intuitive, way. Instead of expressing a quantity as a fraction larger than one, we break it down into a whole number and a remaining fractional part.
Method 1: Long Division
The most straightforward way to convert 12/5 to a mixed number is through long division. This method is applicable to any improper fraction:
-
Divide the numerator by the denominator: Divide 12 (the numerator) by 5 (the denominator).
2 5 | 12 10 -- 2 -
Identify the quotient and remainder: The quotient (the result of the division) is 2, and the remainder is 2.
-
Write the mixed number: The quotient becomes the whole number part of the mixed number, and the remainder becomes the numerator of the fractional part. The denominator remains the same. Therefore, 12/5 = 2 2/5.
Method 2: Visual Representation
Visualizing the fraction can be helpful, especially for beginners. Imagine you have 12 slices of pizza, and each pizza has 5 slices.
-
Group the slices: Group the slices into sets of 5 (because the denominator is 5). You can form two complete pizzas (two sets of 5 slices).
-
Count the remaining slices: After forming two complete pizzas, you'll have 2 slices left over.
-
Write the mixed number: The two complete pizzas represent the whole number (2), and the 2 leftover slices represent the numerator of the fraction (2/5). So, 12/5 = 2 2/5.
Method 3: Repeated Subtraction
This method involves repeatedly subtracting the denominator from the numerator until you reach a number less than the denominator.
-
Subtract the denominator repeatedly: Subtract 5 from 12 until you get a number less than 5:
12 - 5 = 7 7 - 5 = 2
-
Count the subtractions: You subtracted 5 twice (meaning you had 2 whole sets of 5).
-
Write the mixed number: The number of times you subtracted (2) becomes the whole number. The remaining number (2) becomes the numerator, and the denominator (5) remains the same. Thus, 12/5 = 2 2/5.
Converting Other Improper Fractions: Examples
Let's practice with a few more examples to solidify your understanding:
Example 1: 17/3
Using long division:
5
3 | 17
15
--
2
Therefore, 17/3 = 5 2/3.
Example 2: 25/4
Using repeated subtraction:
25 - 4 = 21 21 - 4 = 17 17 - 4 = 13 13 - 4 = 9 9 - 4 = 5 5 - 4 = 1
We subtracted 4 six times, leaving a remainder of 1. Therefore, 25/4 = 6 1/4.
Example 3: 10/10
Using any method, we see that 10/10 simplifies to 1. This highlights the fact that even improper fractions where the numerator and denominator are equal result in a whole number.
Example 4: 22/7
This fraction is already in its simplest form and is an improper fraction. Using long division:
3
7 | 22
21
--
1
Therefore, 22/7 = 3 1/7.
Common Mistakes to Avoid
-
Incorrect division: Ensure you correctly divide the numerator by the denominator. Double-check your calculations.
-
Misinterpreting the remainder: The remainder becomes the numerator of the fractional part, not the whole number.
-
Forgetting the denominator: Remember that the denominator of the fraction in the mixed number remains the same as the denominator of the original improper fraction.
-
Not simplifying the fraction: After converting to a mixed number, always check if the fractional part can be simplified to its lowest terms.
Why Learn to Convert Improper Fractions to Mixed Numbers?
Understanding this conversion is crucial for several reasons:
-
Better comprehension: Mixed numbers are often easier to visualize and understand than improper fractions, especially in real-world contexts (e.g., measuring ingredients in a recipe).
-
Problem-solving: Many mathematical problems require working with mixed numbers, making this conversion a necessary step in the process.
-
Foundation for more advanced math: Mastering this skill is essential for understanding more complex topics like working with decimals, percentages, and more advanced fraction operations.
Conclusion
Converting an improper fraction, such as 12/5, to a mixed number is a fundamental mathematical skill with practical applications. By understanding the concepts behind improper fractions and mixed numbers and applying the various methods outlined in this guide – long division, visual representation, and repeated subtraction – you can confidently perform this conversion and tackle more advanced mathematical challenges. Remember to practice regularly and double-check your work to avoid common mistakes. With consistent practice, this essential skill will become second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 12/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.