Whats 2 To The Power Of 4
News Co
Apr 08, 2025 · 6 min read
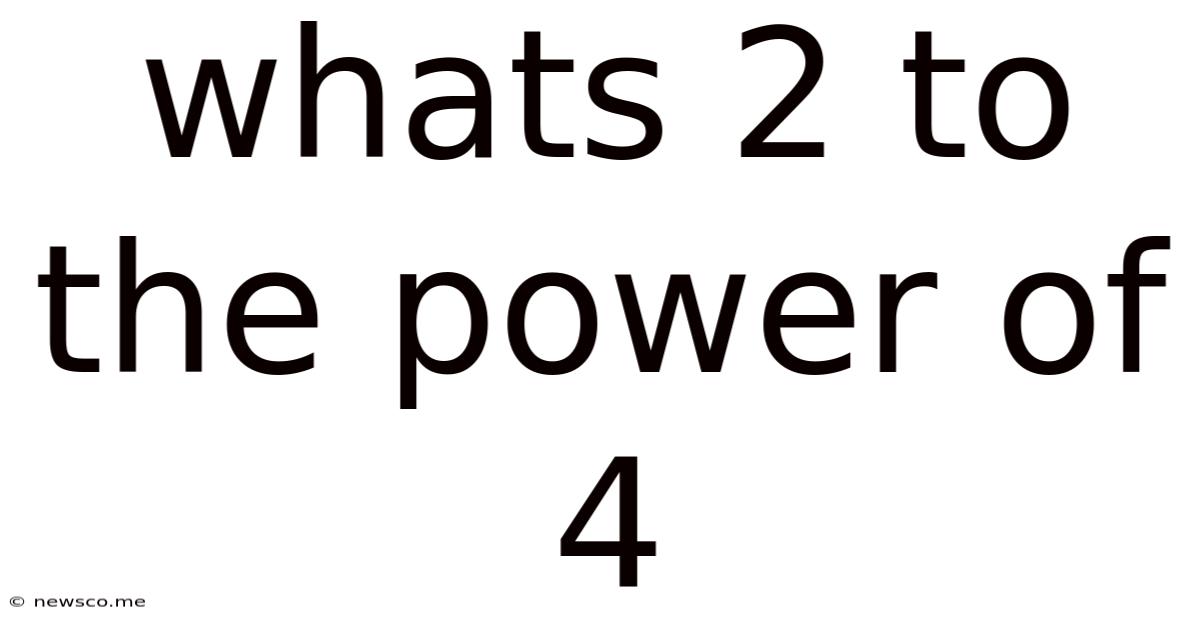
Table of Contents
What's 2 to the Power of 4? Unpacking Exponents and Their Applications
The seemingly simple question, "What's 2 to the power of 4?", opens a door to a vast world of mathematical concepts and their practical applications across various fields. This seemingly basic calculation, represented as 2<sup>4</sup>, serves as a perfect entry point to understand exponents, their properties, and their widespread relevance in computing, finance, science, and everyday life. Let's delve into this seemingly simple problem and uncover its deeper meaning.
Understanding Exponents: A Foundation for Growth
Before we tackle 2<sup>4</sup> specifically, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression b<sup>n</sup>, 'b' is the base and 'n' is the exponent. This means that b<sup>n</sup> represents b multiplied by itself 'n' times.
For instance:
- 2<sup>1</sup> = 2 (2 multiplied by itself once)
- 2<sup>2</sup> = 2 x 2 = 4 (2 multiplied by itself twice)
- 2<sup>3</sup> = 2 x 2 x 2 = 8 (2 multiplied by itself three times)
- 2<sup>4</sup> = 2 x 2 x 2 x 2 = 16 (2 multiplied by itself four times)
Therefore, the answer to "What's 2 to the power of 4?" is 16.
Beyond the Basics: Properties of Exponents
The concept of exponents extends far beyond simple calculations like 2<sup>4</sup>. Understanding the properties of exponents is crucial for more advanced mathematical operations and problem-solving. These properties include:
-
Product of Powers: When multiplying two numbers with the same base, you add their exponents: b<sup>m</sup> x b<sup>n</sup> = b<sup>(m+n)</sup>
-
Quotient of Powers: When dividing two numbers with the same base, you subtract their exponents: b<sup>m</sup> / b<sup>n</sup> = b<sup>(m-n)</sup>
-
Power of a Power: When raising a power to another power, you multiply the exponents: (b<sup>m</sup>)<sup>n</sup> = b<sup>(m x n)</sup>
-
Power of a Product: When raising a product to a power, you raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>
These properties allow us to simplify complex exponential expressions and solve various mathematical problems efficiently.
Applications of Exponents: A World of Possibilities
The concept of exponents isn't confined to the realm of abstract mathematics. It has profound and wide-ranging applications in numerous fields:
1. Computing and Data Storage:
Exponents are fundamental to computer science, particularly in data storage and processing. The size of computer memory is often expressed in powers of 2 (e.g., kilobytes, megabytes, gigabytes, terabytes). Each increment represents a doubling of storage capacity. This is because computers operate using binary code (0s and 1s), making powers of 2 naturally intuitive for data representation. Understanding exponents is crucial for comprehending how data is stored and processed efficiently.
2. Finance and Compound Interest:
Exponential growth is a central concept in finance, especially when dealing with compound interest. Compound interest means earning interest not just on the principal amount but also on accumulated interest. The formula for compound interest involves exponents, illustrating how investments grow over time. The power of compounding highlights the long-term benefits of consistent investment. A small initial investment can grow significantly over decades due to the exponential nature of compound interest. Understanding this allows for more informed financial planning and investment strategies.
3. Science and Engineering:
Exponents are essential across various scientific and engineering disciplines. Exponential functions describe many natural phenomena, including:
-
Population Growth: Population growth often follows an exponential pattern, especially in the early stages. Understanding exponential growth helps model population dynamics and predict future population sizes.
-
Radioactive Decay: The decay of radioactive substances is also described by exponential functions. This knowledge is crucial in various applications, including carbon dating and nuclear medicine.
-
Bacterial Growth: Similar to population growth, bacterial growth often exhibits exponential patterns under optimal conditions. This understanding is critical in microbiology and medicine for controlling bacterial infections and developing effective treatments.
-
Spread of Diseases: The spread of infectious diseases can be modeled using exponential growth functions, helping public health officials understand and manage outbreaks effectively. This understanding is critical for resource allocation and preventative measures.
-
Earthquake Magnitude: The Richter scale, used to measure the magnitude of earthquakes, is a logarithmic scale based on exponents, allowing for a clear representation of the vast range in earthquake intensities.
4. Everyday Life:
While not always explicitly noticeable, exponents are present in many aspects of everyday life:
-
Recipe Scaling: Doubling or tripling a recipe involves multiplying ingredient quantities by powers of 2 or 3.
-
Geometric Progression: Many sequences, like the growth of a chain letter or the pattern of squares on a chessboard, follow a geometric progression, which inherently involves exponents.
Expanding the Scope: Beyond 2<sup>4</sup>
While we've focused on 2<sup>4</sup>, the principles discussed extend to other bases and exponents. Understanding the concept of exponents empowers you to tackle more complex calculations and real-world problems. For example, consider the following:
-
10<sup>3</sup> (10 to the power of 3) = 1000 This demonstrates the concept of powers of 10, crucial in the metric system and scientific notation.
-
3<sup>5</sup> (3 to the power of 5) = 243 This calculation highlights the versatility of exponential notation and its applicability to various bases.
-
e<sup>x</sup> (e to the power of x) This signifies the natural exponential function, an important concept in calculus and many scientific applications. The constant 'e' (approximately 2.718) is a fundamental mathematical constant with widespread implications in growth and decay phenomena.
Conclusion: The Enduring Significance of Exponents
The simple calculation of 2<sup>4</sup> serves as a gateway to a comprehensive understanding of exponents, their properties, and their wide-ranging applications. From computing and finance to science and everyday life, the concept of exponents permeates various facets of our world. Mastering this fundamental mathematical concept opens doors to a deeper appreciation of the mathematical principles underpinning many processes and phenomena around us. Its practical applications are innumerable, highlighting the enduring significance of exponents in both theoretical and applied contexts. The seemingly simple "16" is far more profound than it first appears, embodying a powerful tool for understanding growth, decay, and a multitude of other processes that shape our reality.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 2 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.