Whats 4 To The Power Of 2
News Co
Apr 21, 2025 · 5 min read
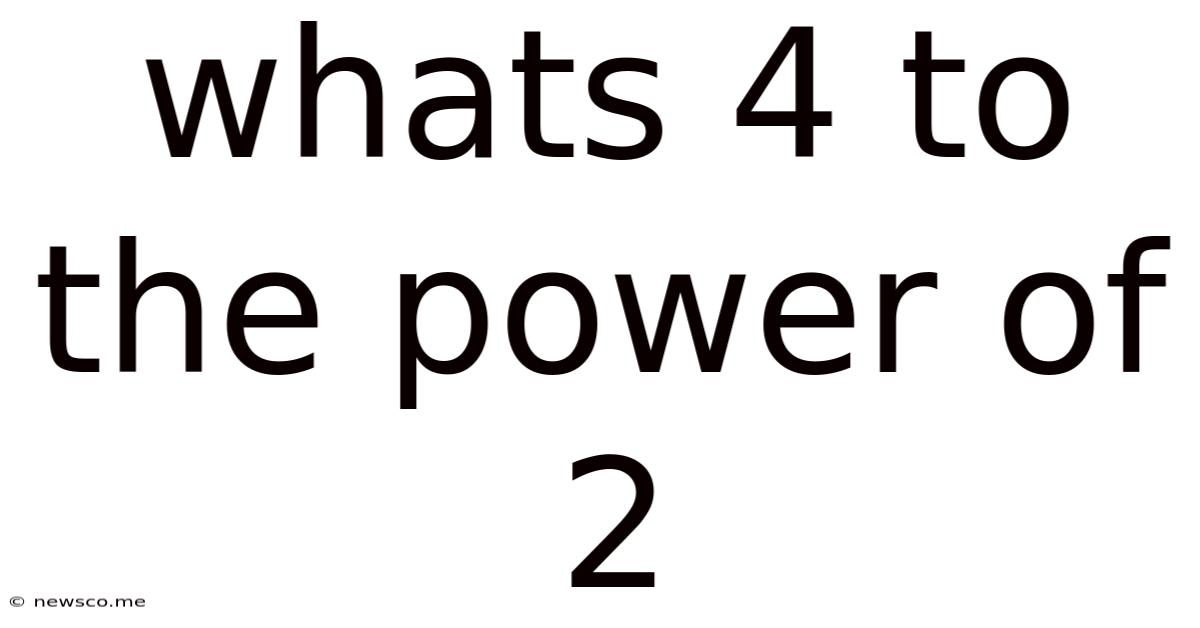
Table of Contents
What's 4 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What's 4 to the power of 2?" opens the door to a fascinating world of mathematics, specifically the concept of exponents. While the answer itself is straightforward (16), understanding the underlying principles and broader applications of exponents is crucial for anyone navigating various fields, from basic arithmetic to advanced calculus and even computer science. This article will not only answer the initial question but delve deep into the concept of exponents, exploring their properties, practical uses, and relevance in various contexts.
Understanding Exponents: The Basics
Before tackling the intricacies of exponents, let's establish a solid foundation. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression 4², the number 4 is the base, and the number 2 is the exponent. Therefore, 4² means 4 multiplied by itself twice: 4 x 4 = 16.
Key Terminology:
- Base: The number being multiplied repeatedly. In 4², 4 is the base.
- Exponent: The number indicating how many times the base is multiplied by itself. In 4², 2 is the exponent.
- Power: Another term for exponent. We often say "4 to the power of 2".
Simple Examples:
- 2³ = 2 x 2 x 2 = 8
- 5¹ = 5 (Any number raised to the power of 1 is itself)
- 10⁰ = 1 (Any non-zero number raised to the power of 0 is 1)
- 3⁻² = 1/(3²) = 1/9 (Negative exponents represent reciprocals)
Beyond the Basics: Properties of Exponents
Exponents follow specific rules or properties that simplify calculations and problem-solving. Understanding these properties is essential for working efficiently with exponential expressions.
1. Product of Powers: When multiplying two powers with the same base, you add the exponents.
- aᵐ x aⁿ = aᵐ⁺ⁿ
Example: 2³ x 2² = 2⁽³⁺²⁾ = 2⁵ = 32
2. Quotient of Powers: When dividing two powers with the same base, you subtract the exponents.
- aᵐ / aⁿ = aᵐ⁻ⁿ (where a ≠ 0)
Example: 5⁵ / 5² = 5⁽⁵⁻²⁾ = 5³ = 125
3. Power of a Power: When raising a power to another power, you multiply the exponents.
- (aᵐ)ⁿ = aᵐⁿ
Example: (3²)³ = 3⁽²ˣ³⁾ = 3⁶ = 729
4. Power of a Product: When raising a product to a power, you raise each factor to that power.
- (ab)ⁿ = aⁿbⁿ
Example: (2 x 3)² = 2² x 3² = 4 x 9 = 36
5. Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power.
- (a/b)ⁿ = aⁿ/bⁿ (where b ≠ 0)
Example: (4/2)³ = 4³/2³ = 64/8 = 8
Real-World Applications of Exponents
Exponents are far from being just a theoretical concept; they have widespread practical applications across numerous fields:
1. Science and Engineering: Exponents are fundamental in expressing scientific notation, a concise way of representing extremely large or small numbers. For instance, the speed of light is approximately 3 x 10⁸ meters per second. Exponents also play a vital role in describing exponential growth and decay, such as population growth, radioactive decay, and compound interest calculations.
2. Finance and Economics: Compound interest, a key concept in finance, relies heavily on exponents. The formula for compound interest involves raising the principal amount to the power of the number of compounding periods. Understanding exponential growth in financial models is crucial for investment strategies and economic forecasting.
3. Computer Science: Binary numbers, the foundation of computer systems, are essentially based on powers of 2. Data storage, memory management, and algorithm design often involve exponential calculations. Moreover, the complexity of algorithms is frequently expressed using Big O notation, which involves exponential functions.
4. Physics: Many physical phenomena are described using exponential functions. For example, the intensity of light decreases exponentially as it travels through a medium, and the decay of radioactive isotopes follows an exponential decay model.
Solving Problems Involving Exponents
Let's explore some practical examples to solidify our understanding of exponents:
Example 1: Simplify the expression (2³ x 2⁻¹)⁴
Using the properties of exponents:
- Combine the bases: 2³ x 2⁻¹ = 2⁽³⁻¹⁾ = 2²
- Raise to the power of 4: (2²)⁴ = 2⁽²ˣ⁴⁾ = 2⁸ = 256
Example 2: Solve for x: 2ˣ = 16
Since 16 is 2⁴, then x = 4.
Example 3: Calculate the compound interest on $1000 invested at an annual rate of 5% for 3 years, compounded annually.
The formula for compound interest is A = P(1 + r/n)^(nt), where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
In this case: P = 1000, r = 0.05, n = 1, and t = 3.
A = 1000(1 + 0.05/1)^(1*3) = 1000(1.05)³ ≈ 1157.63
Therefore, the compound interest earned is approximately $157.63.
Beyond the Simple: More Complex Exponents
While we've primarily focused on integer exponents, exponents can also be fractions (rational exponents) and even irrational numbers (like π or e).
Fractional Exponents: A fractional exponent represents a combination of powers and roots. For example:
- a^(m/n) = ⁿ√(aᵐ)
This means taking the nth root of a raised to the power of m.
Example: 8^(2/3) = ³√(8²) = ³√64 = 4
Conclusion: The Enduring Power of Exponents
The seemingly simple question of "What's 4 to the power of 2?" has served as a gateway to explore the extensive world of exponents. From basic arithmetic to complex scientific models, exponents are fundamental mathematical tools. Understanding their properties and applications is crucial for navigating various fields and solving a wide range of problems. Whether you're calculating compound interest, analyzing scientific data, or programming computer algorithms, the power of exponents is undeniable and pervasive. Mastering this fundamental concept opens doors to a deeper understanding of the mathematical world and its impact on our daily lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 4 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.