Whats 4 To The Power Of 3
News Co
Apr 23, 2025 · 5 min read
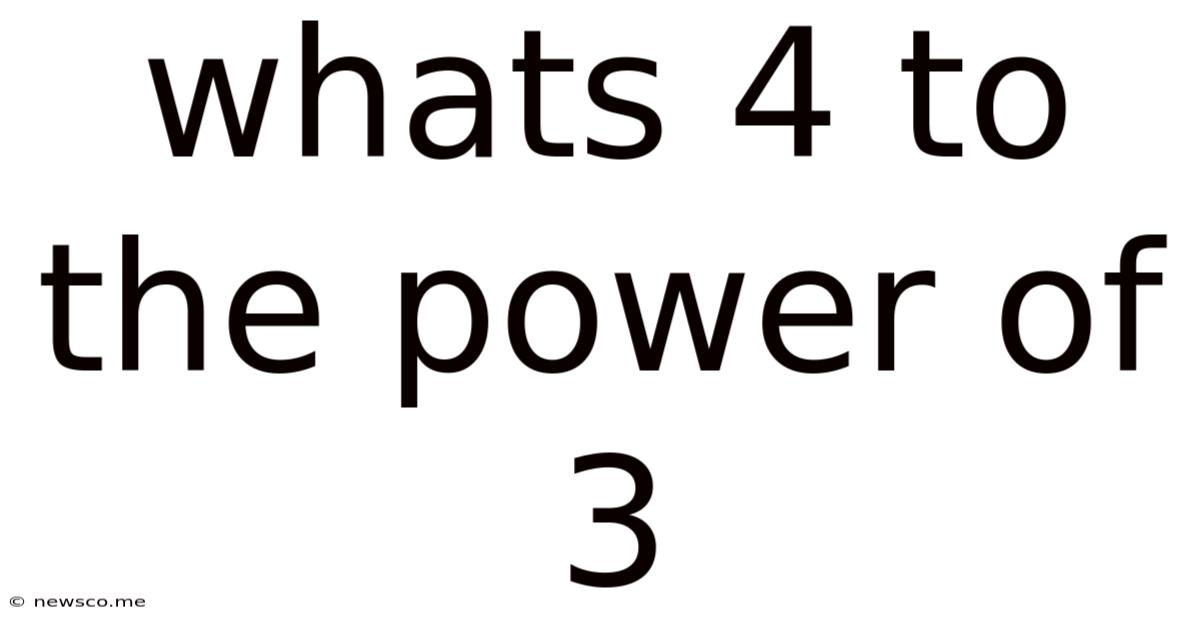
Table of Contents
What's 4 to the Power of 3? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What's 4 to the power of 3?" opens a door to a vast world of mathematical concepts, practical applications, and surprising connections. While the answer itself is straightforward – 64 – the journey to understanding how we arrive at that answer, and the broader implications of exponentiation, is far more enriching. This article will not only answer the initial question but also delve into the fundamentals of exponents, explore their real-world applications, and touch upon some advanced concepts related to exponential growth and decay.
Understanding Exponents: The Basics
Before we tackle 4 to the power of 3, let's establish a firm understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented by a superscript number placed to the right of the base. For instance, in the expression 4³, 4 is the base and 3 is the exponent. This means 4 multiplied by itself three times: 4 × 4 × 4.
The Simple Calculation: 4³
Therefore, to answer the question "What's 4 to the power of 3?", we perform the following calculation:
4 × 4 × 4 = 64
So, 4 to the power of 3 equals 64.
This might seem trivial, but the concept of exponentiation underpins many complex mathematical models and real-world phenomena.
Beyond the Basics: Exploring Exponent Properties
The seemingly simple operation of raising a number to a power actually exhibits a rich set of properties that make it a powerful tool in mathematics and beyond. Let's explore some key properties:
1. Product of Powers:
When multiplying two numbers with the same base, you add their exponents. For example:
4² × 4³ = 4⁽²⁺³⁾ = 4⁵ = 1024
This property is crucial for simplifying complex expressions and solving equations involving exponents.
2. Quotient of Powers:
When dividing two numbers with the same base, you subtract their exponents. For example:
4⁵ ÷ 4² = 4⁽⁵⁻²⁾ = 4³ = 64
This property is useful for reducing fractions with exponential terms.
3. Power of a Power:
When raising a power to another power, you multiply the exponents. For example:
(4²)³ = 4⁽²ˣ³⁾ = 4⁶ = 4096
This property is essential when dealing with nested exponents.
4. Power of a Product:
When raising a product to a power, you raise each factor to that power. For example:
(4 × 2)² = 4² × 2² = 16 × 4 = 64
This simplifies expressions involving multiple terms raised to a power.
5. Power of a Quotient:
Similarly, when raising a quotient to a power, you raise both the numerator and the denominator to that power. For example:
(4/2)² = 4²/2² = 16/4 = 4
Mastering these properties is vital for efficient manipulation of exponential expressions. They are the building blocks for solving more complex problems involving exponents.
Real-World Applications of Exponents
Exponents are not just abstract mathematical concepts; they have far-reaching applications in diverse fields:
1. Compound Interest:
One of the most practical applications of exponents is in calculating compound interest. The formula for compound interest involves exponents:
A = P(1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
This formula demonstrates how exponential growth rapidly increases the value of an investment over time. The exponent (nt) dictates the compounding effect.
2. Population Growth:
Exponential functions are frequently used to model population growth. Under ideal conditions, populations tend to grow exponentially, doubling or tripling within a given timeframe. The formula often used is:
P(t) = P₀e^(rt)
Where:
- P(t) is the population at time t
- P₀ is the initial population
- r is the growth rate
- t is the time
- e is Euler's number (approximately 2.71828)
Understanding exponential growth models helps predict future population sizes and plan for resource allocation.
3. Radioactive Decay:
Conversely, exponential decay models are used to describe the decrease in radioactive material over time. The formula is similar to population growth, but the growth rate (r) is negative, representing decay:
N(t) = N₀e^(-λt)
Where:
- N(t) is the amount of substance remaining after time t
- N₀ is the initial amount of substance
- λ is the decay constant
This model is critical in nuclear physics, environmental science, and carbon dating.
4. Computer Science:
Exponents play a crucial role in computer science, particularly in algorithm analysis. The time complexity of many algorithms is expressed using exponential notation, indicating how the runtime scales with the input size. For example, an algorithm with exponential time complexity (like brute-force password cracking) becomes impractically slow as the input size increases.
5. Physics and Engineering:
From calculating the energy of a photon (E=hc/λ where λ is the wavelength, and the relationship is inversely proportional which uses exponents) to modeling the spread of waves, exponents are fundamental in physics and engineering. They are also used in describing various physical phenomena such as exponential attenuation of signals in communication systems.
Advanced Concepts: Logarithms and Exponential Functions
Understanding exponents opens the door to more advanced mathematical concepts such as logarithms and exponential functions. Logarithms are essentially the inverse operation of exponentiation. They help us solve equations where the unknown is in the exponent. Exponential functions, on the other hand, are functions where the variable is in the exponent, leading to the characteristic exponential growth or decay curves. These concepts are crucial for advanced studies in mathematics, science, and engineering.
Conclusion: The Power of Exponents
While the answer to "What's 4 to the power of 3?" is a simple 64, the underlying principles of exponentiation are far-reaching and profoundly impactful. From calculating compound interest to modeling population growth and radioactive decay, exponents are indispensable tools across various disciplines. Understanding the properties of exponents and their applications empowers us to solve complex problems and interpret real-world phenomena with greater clarity and precision. The journey from a simple calculation to grasping the broader implications of exponentiation highlights the interconnectedness of seemingly disparate fields and the power of mathematical concepts to illuminate our understanding of the world around us. Further exploration of these concepts will invariably lead to a deeper understanding of the world and its intricate workings, unveiling the beauty and power of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 4 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.