Whats 4 To The Power Of 4
News Co
Apr 14, 2025 · 5 min read
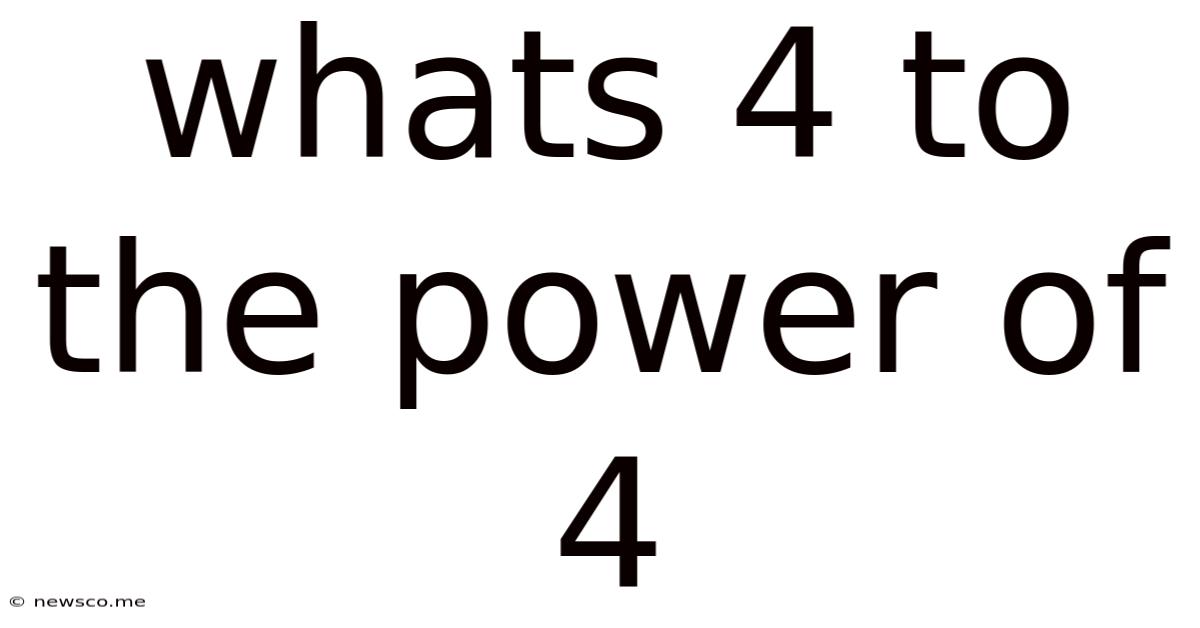
Table of Contents
- Whats 4 To The Power Of 4
- Table of Contents
- What's 4 to the Power of 4? Unpacking Exponents and Their Applications
- Understanding Exponents: A Foundation
- Calculating 4<sup>4</sup>
- Beyond the Basics: Exploring Exponential Growth
- Real-World Examples of Exponential Growth
- The Counterpart: Exponential Decay
- Real-World Examples of Exponential Decay
- Applications of Exponential Functions
- Science and Engineering
- Finance and Economics
- Other Fields
- Beyond 4<sup>4</sup>: Expanding Our Understanding
- Conclusion: The Power of Understanding Exponents
- Latest Posts
- Related Post
What's 4 to the Power of 4? Unpacking Exponents and Their Applications
The seemingly simple question, "What's 4 to the power of 4?" opens a door to a vast world of mathematical concepts, practical applications, and fascinating insights. This article delves deep into understanding exponentiation, exploring what 4<sup>4</sup> actually represents, and examining its relevance across various fields. We'll also touch upon related concepts like exponential growth and decay, and how these principles influence our daily lives.
Understanding Exponents: A Foundation
Before jumping into the calculation of 4<sup>4</sup>, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the general form a<sup>n</sup>, 'a' represents the base, and 'n' represents the exponent. Therefore, 4<sup>4</sup> signifies 4 multiplied by itself four times: 4 × 4 × 4 × 4.
Calculating 4<sup>4</sup>
Now, let's tackle the calculation:
4 × 4 = 16
16 × 4 = 64
64 × 4 = 256
Therefore, 4 to the power of 4 is 256. This simple calculation forms the bedrock for understanding more complex exponential expressions.
Beyond the Basics: Exploring Exponential Growth
The concept of exponentiation is fundamental to understanding exponential growth, a phenomenon where a quantity increases at a rate proportional to its current value. This type of growth is characterized by a rapid increase over time, often visualized as a steep upward curve on a graph.
Real-World Examples of Exponential Growth
Exponential growth is ubiquitous in our world. Consider these examples:
-
Population growth: Under ideal conditions, populations of organisms (bacteria, animals, humans) can exhibit exponential growth. Each individual contributes to the overall population growth, leading to a rapidly increasing total.
-
Compound interest: The magic of compound interest is based on exponential growth. Interest earned is added to the principal amount, and subsequent interest is calculated on the larger sum, leading to accelerated growth over time. This is why starting investments early is so crucial.
-
Viral spread: The spread of viral information or diseases often follows an exponential pattern. Each infected individual can potentially infect multiple others, leading to an exponential increase in the number of infected individuals.
-
Technological advancements: The pace of technological advancements often follows an exponential trajectory. Each innovation can build upon previous ones, accelerating the overall rate of progress.
The Counterpart: Exponential Decay
While exponential growth focuses on increases, exponential decay describes situations where a quantity decreases at a rate proportional to its current value. This results in a gradual decline, often visualized as a downward curve that approaches zero asymptotically.
Real-World Examples of Exponential Decay
Similar to exponential growth, exponential decay is prevalent in many aspects of life:
-
Radioactive decay: Radioactive materials decay at an exponential rate, with their half-life representing the time it takes for half of the material to decay. This principle is crucial in various fields, including medicine and nuclear energy.
-
Drug metabolism: The body metabolizes many drugs at an exponential rate. The concentration of the drug in the bloodstream decreases over time.
-
Cooling of objects: The rate at which an object cools down is often exponential, approaching the ambient temperature asymptotically.
Applications of Exponential Functions
Understanding exponentiation and its related concepts – exponential growth and decay – has wide-ranging applications across various fields:
Science and Engineering
-
Physics: Exponential functions are fundamental in describing phenomena like radioactive decay, capacitor discharge, and the damping of oscillations.
-
Chemistry: Chemical reactions often follow exponential rate laws, allowing scientists to model and predict reaction kinetics.
-
Biology: Population dynamics, drug metabolism, and the spread of diseases are all areas where exponential functions play a critical role.
-
Computer Science: Algorithms, data structures, and computational complexity analyses often involve exponential functions, providing insights into efficiency and scalability.
Finance and Economics
-
Compound interest: As mentioned earlier, compound interest calculations rely heavily on exponential functions.
-
Investment growth: Predicting the growth of investments and understanding the impact of compounding are crucial for financial planning.
-
Economic modeling: Exponential functions are used in macroeconomic models to study various economic phenomena, such as inflation and economic growth.
Other Fields
-
Medicine: Drug dosage calculations, modeling disease spread, and understanding biological processes often utilize exponential functions.
-
Environmental Science: Modeling pollution spread, population growth of invasive species, and resource depletion involve exponential concepts.
-
Social Sciences: Diffusion of innovations, the spread of rumors, and social network growth can all be modeled using exponential functions.
Beyond 4<sup>4</sup>: Expanding Our Understanding
While we’ve focused on 4<sup>4</sup>, the principles discussed extend far beyond this specific calculation. The concept of exponentiation is a cornerstone of mathematics, forming the basis for logarithms, complex numbers, and many other advanced mathematical concepts. Mastering exponentiation provides a solid foundation for tackling more complex mathematical challenges.
Conclusion: The Power of Understanding Exponents
The seemingly simple question, "What's 4 to the power of 4?" has led us on a journey through the fascinating world of exponents, exponential growth and decay, and their wide-ranging applications. Understanding these concepts not only enhances mathematical proficiency but also provides a framework for comprehending numerous phenomena in the world around us. From predicting population growth to understanding financial investments and modeling the spread of diseases, the power of exponents is undeniable. By grasping these fundamental principles, we equip ourselves with powerful tools for analyzing, interpreting, and predicting the behaviour of complex systems. The seemingly straightforward 256 represents far more than a simple arithmetic answer; it signifies the gateway to a deeper comprehension of exponential relationships pervasive throughout our lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats 4 To The Power Of 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.