What's Half Of 1 And 3/4
News Co
Apr 12, 2025 · 5 min read
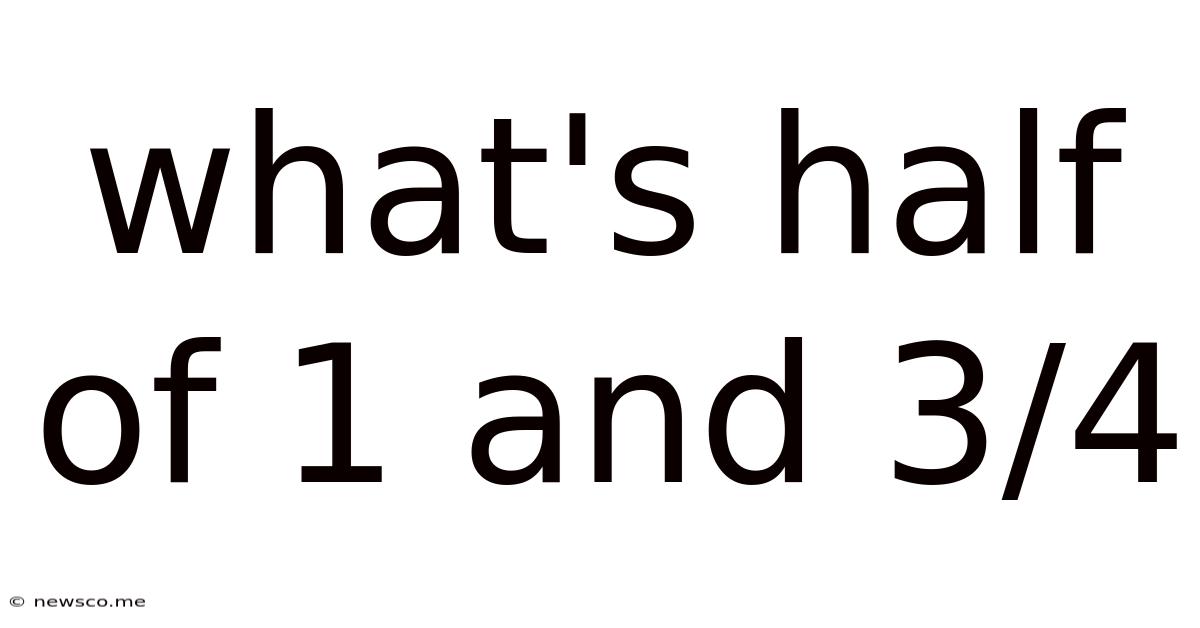
Table of Contents
What's Half of 1 and 3/4? A Deep Dive into Fractions and Division
Finding half of a mixed number like 1 and 3/4 might seem daunting at first, but it's a straightforward process once you understand the underlying principles of fractions and division. This article will not only show you how to calculate half of 1 and 3/4 but also explore the broader concepts involved, providing you with the skills to tackle similar problems confidently. We’ll delve into various methods, ensuring you grasp the fundamental mathematical concepts.
Understanding Mixed Numbers and Improper Fractions
Before we begin, let's clarify some terminology. A mixed number combines a whole number and a fraction, like 1 and 3/4. An improper fraction, on the other hand, has a numerator (top number) larger than or equal to its denominator (bottom number). Understanding the interplay between these two forms is crucial for fraction manipulation.
Converting Mixed Numbers to Improper Fractions
To easily work with mixed numbers in division, it's best to convert them into improper fractions. The process is simple:
- Multiply the whole number by the denominator: In our example, 1 (whole number) x 4 (denominator) = 4.
- Add the numerator: Add the result from step 1 to the numerator of the fraction: 4 + 3 (numerator) = 7.
- Keep the same denominator: The denominator remains unchanged, which is 4 in this case.
Therefore, 1 and 3/4 converts to the improper fraction 7/4.
Calculating Half of 1 and 3/4: Different Approaches
Now, let's explore different methods to calculate half of 1 and 3/4 (or 7/4).
Method 1: Direct Division
The most straightforward approach involves directly dividing the improper fraction by 2. Remember, dividing by 2 is the same as multiplying by 1/2.
- Multiply the numerator by 1: 7 x 1 = 7
- Multiply the denominator by 2: 4 x 2 = 8
This gives us the fraction 7/8. Therefore, half of 1 and 3/4 is 7/8.
Method 2: Dividing the Whole Number and Fraction Separately
This method offers a more intuitive understanding for those who prefer working with mixed numbers directly.
- Find half of the whole number: Half of 1 is 1/2.
- Find half of the fraction: Half of 3/4 is (3/4) / 2 = 3/8.
- Combine the results: Add the results from steps 1 and 2: 1/2 + 3/8. To add these fractions, find a common denominator (8): (4/8) + (3/8) = 7/8.
Again, we arrive at the answer: 7/8.
Method 3: Using Decimal Representation
Another approach involves converting the mixed number into a decimal, finding half of the decimal, and then converting the result back into a fraction (if necessary).
- Convert the mixed number to a decimal: 1 and 3/4 is equal to 1.75.
- Divide by 2: 1.75 / 2 = 0.875.
- Convert the decimal back to a fraction: 0.875 can be expressed as 7/8.
This method reinforces the equivalence of fractions and decimals. The answer, once again, is 7/8.
Expanding the Concept: Halving Other Mixed Numbers
The techniques described above can be applied to any mixed number. Let's illustrate with another example: What's half of 2 and 2/3?
- Convert to an improper fraction: 2 and 2/3 becomes (2 x 3 + 2) / 3 = 8/3.
- Divide by 2 (or multiply by 1/2): (8/3) x (1/2) = 8/6.
- Simplify the fraction: 8/6 simplifies to 4/3.
- Convert back to a mixed number (optional): 4/3 is equal to 1 and 1/3.
Therefore, half of 2 and 2/3 is 4/3 or 1 and 1/3.
Practical Applications and Real-World Examples
Understanding how to find half of a mixed number isn't just a mathematical exercise; it has practical applications in various real-world scenarios:
- Cooking and Baking: Recipes often require halving or doubling ingredients. If a recipe calls for 1 and 3/4 cups of flour, you'll need to know how to calculate half that amount.
- Construction and Measurement: Precise measurements are crucial in construction. Dividing lengths or quantities often involves working with fractions.
- Finance and Budgeting: Calculating half of a budget allocation or dividing expenses might involve mixed numbers.
- Sewing and Crafting: Cutting fabrics or other materials often necessitates working with fractional measurements.
Troubleshooting Common Mistakes
While the process is relatively straightforward, several common mistakes can occur when working with fractions:
- Incorrect conversion to improper fractions: Ensure you're accurately multiplying the whole number by the denominator and adding the numerator.
- Errors in multiplication or division: Double-check your calculations to avoid simple arithmetic mistakes.
- Forgetting to simplify fractions: Always simplify your final answer to its lowest terms.
Conclusion: Mastering Fractions for Everyday Life
Mastering the ability to calculate half of a mixed number—and fractions in general—is an invaluable skill with numerous real-world applications. By understanding the different methods and potential pitfalls, you can confidently tackle such problems and apply these skills to various situations. This comprehensive guide provides a solid foundation for further exploration of fractional arithmetic and builds a strong understanding of mathematical concepts crucial for everyday life. Remember to practice regularly to reinforce your understanding and improve your proficiency in working with fractions. The more you practice, the more intuitive and comfortable you'll become with these essential mathematical operations. From baking cakes to constructing buildings, the ability to work with fractions seamlessly enhances your problem-solving capabilities across a wide range of domains.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's Half Of 1 And 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.