What's The Difference Between Integers And Whole Numbers
News Co
Apr 03, 2025 · 5 min read
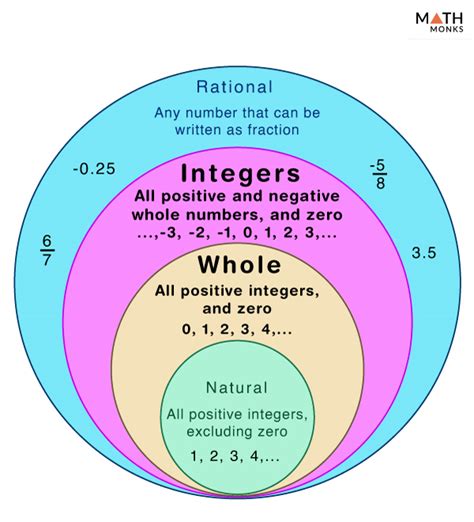
Table of Contents
What's the Difference Between Integers and Whole Numbers? A Deep Dive
Understanding the nuances of mathematical concepts is crucial for anyone pursuing studies or careers involving numbers. While the terms "integers" and "whole numbers" are often used interchangeably, a subtle yet significant difference exists between them. This article will delve into the definitions, explore their properties, and provide practical examples to clarify the distinction. By the end, you'll have a firm grasp of these fundamental mathematical concepts and be able to confidently apply your knowledge.
Defining Whole Numbers
Whole numbers represent the set of non-negative numbers starting from zero and extending infinitely. This means they include 0, 1, 2, 3, and so on. These numbers are often used in everyday counting and represent quantities of discrete objects. Think about the number of apples in a basket, the number of cars in a parking lot, or the number of students in a classroom. These are all scenarios where whole numbers are perfectly applicable.
Key Characteristics of Whole Numbers:
- Non-negative: Whole numbers do not include negative values.
- Discrete: They represent distinct, countable quantities.
- Starting point: The set of whole numbers begins with zero.
- Infinite: The sequence extends indefinitely, without an upper limit.
Defining Integers
Integers, on the other hand, encompass a broader range of numbers. They include all whole numbers (0, 1, 2, 3...) along with their negative counterparts (-1, -2, -3...). This means integers represent both positive and negative whole numbers, including zero.
Key Characteristics of Integers:
- Positive, negative, and zero: Integers include numbers on both sides of zero on the number line.
- Discrete: Like whole numbers, integers represent distinct, countable quantities.
- Infinite in both directions: The integer sequence extends infinitely in both the positive and negative directions.
- Subsets: Whole numbers are a subset of integers; all whole numbers are also integers, but not all integers are whole numbers.
Visualizing the Difference: The Number Line
A number line provides a helpful visual representation of the relationship between whole numbers and integers.
Imagine a line stretching infinitely in both directions. The point in the middle is marked as 0. To the right of 0, we find the positive whole numbers (1, 2, 3...). To the left of 0, we find their negative counterparts (-1, -2, -3...). The whole numbers occupy the non-negative portion of this line, while the integers extend across the entire line, encompassing both positive and negative values.
Therefore: The set of whole numbers is entirely contained within the set of integers.
Practical Examples to Illustrate the Difference
Let's examine scenarios where the distinction between integers and whole numbers becomes crucial:
Scenario 1: Temperature
The temperature outside can be represented using integers. For example, 25°C (positive integer) represents a warm day, while -5°C (negative integer) represents a cold day. While we wouldn't usually describe temperature in terms of whole numbers alone (as it's unlikely to be exactly 0°C), the integers allow for the expression of both positive and negative values.
Scenario 2: Bank Account Balance
Your bank account balance can be represented using integers. A positive balance (e.g., $100) indicates money in your account, while a negative balance (e.g., -$50) indicates you owe the bank money. Whole numbers alone cannot fully describe the state of your account.
Scenario 3: Elevation
Elevation relative to sea level is often expressed using integers. A positive elevation (e.g., 1500 meters above sea level) indicates a height above sea level, while a negative elevation (e.g., -50 meters below sea level) indicates a point below sea level. Whole numbers wouldn’t accurately depict elevations below sea level.
Scenario 4: Counting Objects
When counting the number of physical objects (apples, chairs, books), you would use whole numbers. You can't have a negative number of apples. This is a key scenario where whole numbers perfectly reflect the situation.
Beyond the Basics: Expanding the Number System
While whole numbers and integers form the foundation of many mathematical concepts, they are just the beginning. As we progress in mathematics, we encounter even more expansive number systems:
-
Rational Numbers: These include all numbers that can be expressed as a fraction (a/b), where 'a' and 'b' are integers and 'b' is not zero. This includes integers, as an integer can be expressed as a fraction (e.g., 3 = 3/1). It also includes decimals that terminate (like 0.25) or repeat (like 0.333...).
-
Irrational Numbers: These numbers cannot be expressed as a fraction of two integers. Famous examples include π (pi) and the square root of 2.
-
Real Numbers: This set encompasses all rational and irrational numbers. It represents all numbers on the number line.
-
Complex Numbers: These numbers involve the imaginary unit 'i', which is defined as the square root of -1.
Conclusion: Understanding the Crucial Distinction
The difference between integers and whole numbers might seem subtle at first, but it is fundamentally important. Whole numbers are a subset of integers, focusing exclusively on non-negative values and used primarily for counting. Integers broaden the scope to include negative values, allowing for the representation of quantities and measurements beyond simple counting.
This understanding provides a solid groundwork for further explorations into more advanced mathematical concepts. The ability to distinguish between integers and whole numbers is a critical skill for anyone aiming to understand and apply mathematical principles effectively. By mastering this fundamental difference, you lay a strong foundation for future learning and problem-solving. Remember the key takeaway: all whole numbers are integers, but not all integers are whole numbers. This simple statement encapsulates the core difference between these two essential sets of numbers. Keep practicing and soon you'll be confidently working with integers and whole numbers in any mathematical context.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Difference Between Integers And Whole Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.