What's The Greatest Common Factor Of 12 And 18
News Co
Apr 14, 2025 · 6 min read
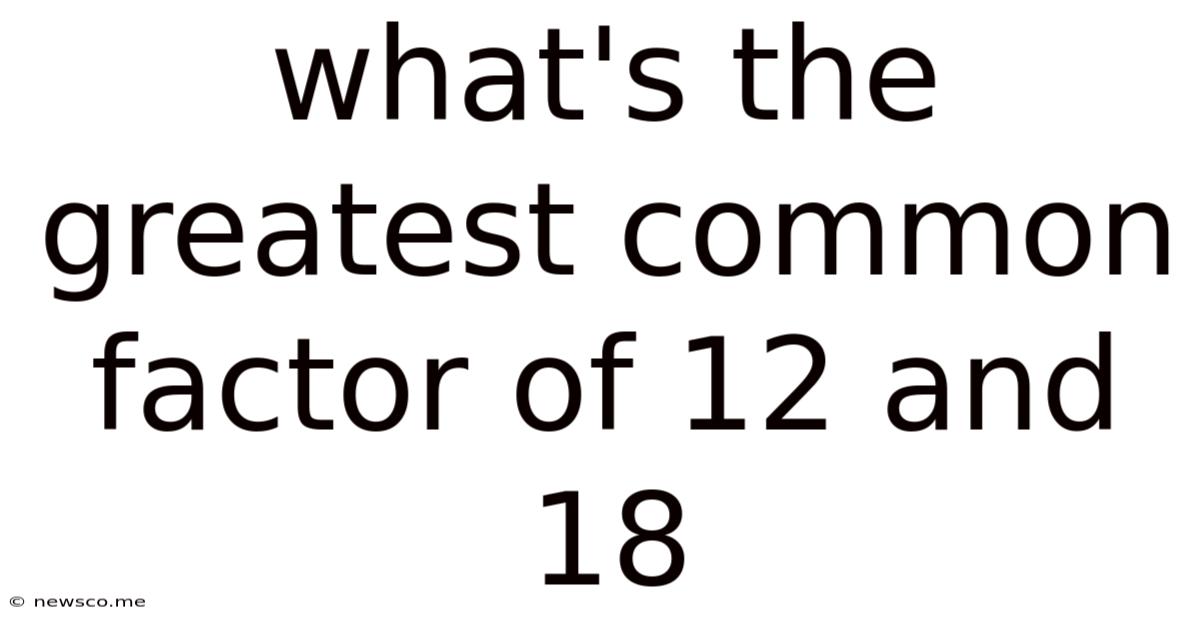
Table of Contents
What's the Greatest Common Factor of 12 and 18? A Deep Dive into Finding GCF
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts and different methods can be surprisingly insightful. This article delves deep into determining the GCF of 12 and 18, exploring various approaches and highlighting their practical applications in mathematics and beyond. We'll move beyond simply stating the answer and explore the why behind the calculations, making this a resource both for students grappling with the concept and those looking for a refresher on fundamental mathematical principles.
Understanding Greatest Common Factors (GCF)
Before we tackle the specific case of 12 and 18, let's establish a solid understanding of what a greatest common factor actually is. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. It's also sometimes called the greatest common divisor (GCD). Understanding this definition is crucial to mastering the methods we'll explore later.
Key Concepts:
- Factors: Factors of a number are whole numbers that divide the number evenly. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Common Factors: Common factors are factors shared by two or more numbers. For instance, 1, 2, 3, and 6 are common factors of 12 and 18.
- Greatest Common Factor (GCF): The largest of these common factors is the greatest common factor.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 12 and 18. We simply list all the factors of each number and then identify the largest factor they have in common.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 18: 1, 2, 3, 6, 9, 18
By comparing the two lists, we can clearly see that the common factors are 1, 2, 3, and 6. The largest of these is 6. Therefore, the GCF of 12 and 18 is 6.
This method works well for smaller numbers, but it becomes less efficient and more prone to error as the numbers get larger.
Method 2: Prime Factorization
This method utilizes the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 12 and 18:
- 12: 2 x 2 x 3 = 2² x 3
- 18: 2 x 3 x 3 = 2 x 3²
Now, we identify the common prime factors and their lowest powers:
- Common prime factors: 2 and 3
- Lowest power of 2: 2¹ = 2
- Lowest power of 3: 3¹ = 3
To find the GCF, we multiply these common prime factors raised to their lowest powers: 2 x 3 = 6.
This method is more efficient than listing factors, particularly for larger numbers, as it systematically breaks down the numbers into their prime components.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 12 and 18:
- Start with the larger number (18) and the smaller number (12): 18 and 12
- Subtract the smaller number from the larger number: 18 - 12 = 6
- Replace the larger number with the result (6) and keep the smaller number (12): 12 and 6
- Repeat the subtraction: 12 - 6 = 6
- The numbers are now equal (6 and 6), so the GCF is 6.
The Euclidean algorithm provides a systematic and efficient way to find the GCF, even for very large numbers, and it's a cornerstone of number theory.
Applications of Finding the GCF
Finding the greatest common factor is not just an abstract mathematical exercise; it has practical applications in various fields:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 12/18 can be simplified by dividing both the numerator and denominator by their GCF, which is 6, resulting in the simplified fraction 2/3.
-
Solving Word Problems: Many word problems in mathematics, especially those involving division and distribution, require finding the GCF to solve efficiently. For instance, if you have 12 apples and 18 oranges, and you want to divide them into identical groups, the GCF (6) determines the maximum number of identical groups you can create.
-
Geometry and Measurement: GCF finds application in geometric problems, like determining the dimensions of the largest square tile that can perfectly cover a rectangular floor of dimensions 12 units by 18 units.
-
Computer Science: The Euclidean algorithm, used for finding the GCF, is a fundamental algorithm in computer science and cryptography, used in various computations and security protocols.
Beyond the Basics: Extending the Concept
While we've focused on finding the GCF of two numbers, the concept extends to finding the GCF of three or more numbers. The methods described above can be adapted to handle this. For example, to find the GCF of 12, 18, and 24, you could use prime factorization or the Euclidean algorithm iteratively.
-
Prime Factorization Method for Multiple Numbers: Find the prime factorization of each number (12 = 2² x 3, 18 = 2 x 3², 24 = 2³ x 3). Identify the common prime factors and their lowest powers (2¹ and 3¹). The GCF is 2 x 3 = 6.
-
Euclidean Algorithm for Multiple Numbers: You can extend the Euclidean algorithm to multiple numbers by finding the GCF of two numbers initially and then finding the GCF of the result and the next number, continuing this process until all numbers are considered.
Conclusion: The Power of Understanding GCF
The seemingly simple task of finding the greatest common factor of 12 and 18 offers a glimpse into the rich world of number theory and its practical applications. By understanding the different methods – listing factors, prime factorization, and the Euclidean algorithm – you gain not just a solution to a specific problem but a deeper appreciation for the fundamental principles of mathematics. This knowledge extends far beyond simple arithmetic, proving valuable in various fields and problem-solving scenarios. The GCF, therefore, is more than just a number; it's a key that unlocks a deeper understanding of mathematical relationships. Mastering the GCF empowers you with problem-solving skills that are applicable across a multitude of disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Greatest Common Factor Of 12 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.