What's The Square Root Of 27
News Co
Apr 05, 2025 · 5 min read
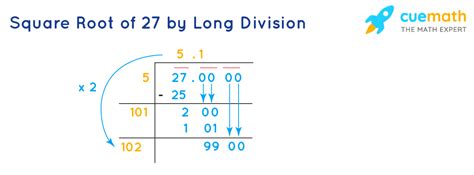
Table of Contents
What's the Square Root of 27? A Deep Dive into Square Roots and Radical Simplification
The question, "What's the square root of 27?" might seem simple at first glance. However, exploring this seemingly straightforward mathematical concept opens the door to a deeper understanding of square roots, radical simplification, and even the nature of numbers themselves. This article will provide a comprehensive answer, exploring not just the numerical solution but also the underlying mathematical principles.
Understanding Square Roots
Before diving into the square root of 27, let's solidify our understanding of what a square root actually represents. The square root of a number (represented by the symbol √) is a value that, when multiplied by itself, gives the original number. For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
- √25 = 5 because 5 * 5 = 25
This concept is fundamentally tied to the idea of squaring a number (raising it to the power of 2). Squaring and taking the square root are inverse operations; they undo each other.
Perfect Squares and Imperfect Squares
Numbers like 9, 16, and 25 are considered perfect squares because their square roots are whole numbers. However, many numbers don't have whole number square roots. These are called imperfect squares. 27 falls into this category. Its square root is not a whole number, but rather an irrational number.
Calculating the Square Root of 27
While a calculator readily provides an approximate decimal value for √27 (approximately 5.196), a more insightful approach involves simplifying the radical. This process reveals the underlying structure of the number and avoids relying solely on a calculator's approximation.
Prime Factorization: The Key to Simplification
The key to simplifying the square root of 27 lies in its prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
Let's find the prime factorization of 27:
27 = 3 x 9 = 3 x 3 x 3 = 3³
Therefore, the prime factorization of 27 is 3³.
Simplifying the Radical Expression
Now, we can rewrite √27 using the prime factorization:
√27 = √(3³)
Since √(a²) = a, we can simplify this expression:
√(3³) = √(3² x 3) = √(3²) x √3 = 3√3
Therefore, the simplified form of √27 is 3√3. This is an exact representation, unlike the decimal approximation provided by a calculator. This form is preferred in many mathematical contexts because it maintains precision and avoids rounding errors.
Understanding Irrational Numbers
The presence of √3 in our simplified answer highlights the nature of √27 as an irrational number. Irrational numbers cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating and non-repeating, meaning they go on forever without a discernible pattern.
This is in contrast to rational numbers, which can be expressed as fractions. For example, 0.5 is rational because it's equivalent to ½.
The irrational nature of √27 is why we often prefer the simplified radical form (3√3) over its decimal approximation. The radical form conveys the exact value without loss of information.
Applications of Square Roots
Understanding square roots extends far beyond basic mathematics. They find applications in numerous fields, including:
Geometry: Calculating Distances and Areas
Square roots are fundamental in geometry, particularly when calculating distances (using the Pythagorean theorem) and areas (for example, finding the side length of a square given its area).
Physics: Velocity and Acceleration Calculations
Square roots appear extensively in physics, especially in calculations involving velocity, acceleration, and energy. For instance, the formula for kinetic energy involves a square root.
Engineering: Structural Design and Calculations
Engineers rely heavily on square roots in structural design and calculations to ensure stability and safety. Many engineering formulas incorporate square roots.
Computer Graphics and Game Development
In the world of computer graphics and game development, square roots are essential for calculations related to distance, transformations, and lighting.
Finance: Calculating Investment Returns and Risk
Even in finance, square roots play a role, particularly in calculating investment returns and assessing risk.
Advanced Concepts Related to Square Roots
Our exploration of √27 touches upon several advanced mathematical concepts worth briefly exploring:
nth Roots: Generalization of Square Roots
Square roots are a specific case of nth roots. The nth root of a number is a value that, when multiplied by itself n times, gives the original number. For example, the cube root (3rd root) of 8 is 2 because 2 * 2 * 2 = 8.
Complex Numbers: Extending the Number System
The concept of square roots extends beyond real numbers to include complex numbers. Complex numbers involve the imaginary unit i, where i² = -1. For example, the square root of -1 is i. While √27 doesn't directly involve complex numbers, understanding this broader context is valuable for deeper mathematical studies.
Approximating Square Roots: Numerical Methods
Various numerical methods exist for approximating square roots, particularly when dealing with numbers that don't have easily simplified radical forms. These methods often involve iterative processes that refine an initial approximation to obtain a more accurate result. Examples include the Babylonian method and the Newton-Raphson method.
Conclusion: More Than Just a Number
The seemingly simple question, "What's the square root of 27?" leads to a rich exploration of mathematical concepts. While the answer is 3√3, understanding how to arrive at this simplified radical form, the nature of irrational numbers, and the various applications of square roots is crucial for a deeper appreciation of mathematics and its relevance in various fields. This exploration highlights the importance of not just calculating answers, but understanding the underlying principles that govern them. This approach fosters deeper learning and a more intuitive grasp of mathematical concepts. Furthermore, the ability to simplify radical expressions is a valuable skill for higher-level mathematical pursuits, highlighting the significance of mastering the fundamentals.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.