Whats The Square Root Of 289
News Co
Apr 03, 2025 · 5 min read
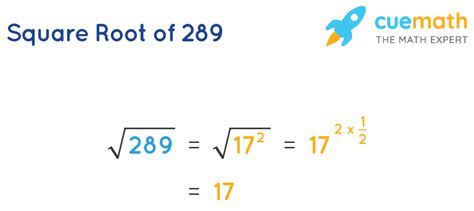
Table of Contents
What's the Square Root of 289? A Deep Dive into Square Roots and Their Applications
The seemingly simple question, "What's the square root of 289?" opens a door to a fascinating world of mathematics, encompassing fundamental concepts, practical applications, and even historical context. This article will not only answer that question definitively but will also explore the broader significance of square roots and their role in various fields.
Understanding Square Roots: The Basics
Before we delve into the specific square root of 289, let's establish a solid understanding of the concept itself. A square root of a number is a value that, when multiplied by itself, equals the original number. In mathematical terms: if x² = y, then x is the square root of y (√y = x).
For example:
- The square root of 9 (√9) is 3, because 3 x 3 = 9.
- The square root of 16 (√16) is 4, because 4 x 4 = 16.
It's important to note that most numbers have two square roots: a positive and a negative one. However, when we talk about "the" square root, we usually refer to the principal square root, which is the positive value.
Calculating the Square Root of 289
Now, let's tackle the question at hand: What is the square root of 289?
There are several ways to calculate this:
1. Manual Calculation (Prime Factorization)
One method involves prime factorization. We break down 289 into its prime factors:
289 = 17 x 17
Since 289 is a perfect square (a number that can be obtained by squaring an integer), its square root is simply one of its prime factors:
√289 = 17
Therefore, the square root of 289 is 17.
2. Using a Calculator
The easiest and most efficient method for finding the square root of 289 is using a calculator. Simply enter 289 and press the square root button (√). The calculator will instantly return the answer: 17.
3. Estimation and Approximation
While less precise, estimation can be a useful skill. We know that 15² = 225 and 20² = 400. Since 289 falls between these two squares, we can deduce that the square root of 289 will be between 15 and 20. Further refinement through trial and error or linear interpolation could lead to a closer approximation, but the calculator method is far more efficient for accurate results.
The Significance of Square Roots in Mathematics
Square roots are fundamental in various mathematical concepts and operations:
-
Pythagorean Theorem: This theorem, a cornerstone of geometry, states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Solving for the length of a side often requires calculating a square root.
-
Quadratic Equations: These equations, of the form ax² + bx + c = 0, often involve square roots in their solutions, using the quadratic formula.
-
Coordinate Geometry: Distance calculations between points on a coordinate plane utilize the distance formula, which relies on square roots.
-
Calculus: Square roots appear frequently in calculus, particularly in differentiation and integration.
-
Trigonometry: Certain trigonometric identities and formulas involve square roots.
Applications of Square Roots in Real-World Scenarios
The applications of square roots extend far beyond the realm of pure mathematics. They are crucial in numerous fields:
-
Physics: Calculations involving velocity, acceleration, and energy often require the use of square roots. For example, calculating the speed of an object requires extracting the square root of the kinetic energy.
-
Engineering: Designing structures, calculating stresses and strains, and solving problems related to mechanics frequently rely on square root calculations.
-
Construction: Determining distances and dimensions, particularly when dealing with right angles (as in the Pythagorean Theorem), is vital in construction.
-
Computer Graphics: Generating and manipulating images and 3D models rely heavily on coordinate geometry and vector calculations, which involve square roots.
-
Finance: Certain financial calculations, such as calculating standard deviation in investment analysis, utilize square roots.
-
Statistics: Finding standard deviation, a key measure of data dispersion, involves calculating a square root.
Historical Context: The Evolution of Square Root Calculation
The concept of square roots has been understood and utilized for millennia. Ancient Babylonian mathematicians, as early as the 20th century BCE, developed methods for approximating square roots. The Greeks, too, made significant contributions to the understanding and calculation of square roots, with figures like Pythagoras exploring their geometric properties. Over time, more refined methods and algorithms have been developed, culminating in the efficient computational methods we use today.
Beyond the Basics: Exploring Complex Numbers
While we've focused on the square roots of positive real numbers, it's worth briefly mentioning the concept of complex numbers. The square root of a negative number is not a real number but an imaginary number, denoted by 'i', where i² = -1. Complex numbers combine real and imaginary components, expanding the scope of mathematical operations and enabling the solving of a wider range of equations.
Conclusion: The Enduring Importance of Square Roots
The seemingly straightforward question, "What's the square root of 289?" leads to a much broader understanding of a core mathematical concept with far-reaching implications. From fundamental geometric principles to advanced calculations in various scientific and engineering disciplines, square roots play a crucial role in shaping our understanding of the world around us. Their continued importance highlights the enduring power and relevance of fundamental mathematical concepts in a constantly evolving world. Mastering the concept of square roots, therefore, represents more than just a mathematical skill; it's a fundamental building block for understanding numerous other mathematical and scientific concepts and applications. The simple answer of 17 is just the beginning of a deeper exploration into a fascinating field.
Latest Posts
Related Post
Thank you for visiting our website which covers about Whats The Square Root Of 289 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.