What's The Square Root Of 500
News Co
Apr 05, 2025 · 5 min read
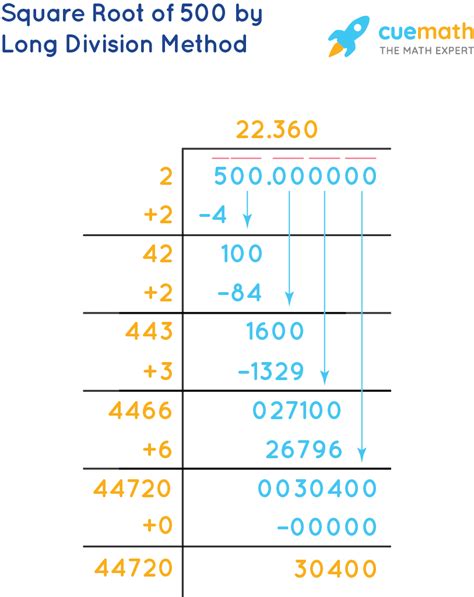
Table of Contents
What's the Square Root of 500? A Deep Dive into Square Roots and Approximation Techniques
The seemingly simple question, "What's the square root of 500?" opens a door to a fascinating world of mathematical concepts, approximation techniques, and the power of computational tools. While a calculator readily provides the decimal approximation, understanding the underlying principles offers a richer appreciation of mathematics and its applications. This article delves into the square root of 500, exploring various methods to determine its value, discussing the history of square root calculations, and examining practical applications of this fundamental mathematical operation.
Understanding Square Roots
Before we tackle the specific case of the square root of 500, let's establish a foundational understanding of square roots. A square root of a number is a value that, when multiplied by itself (squared), equals the original number. For instance, the square root of 9 is 3, because 3 x 3 = 9. This is often expressed mathematically as √9 = 3.
Key Concepts:
- Perfect Squares: These are numbers that result from squaring an integer (whole number). Examples include 4 (2²), 9 (3²), 16 (4²), and so on. 500 is not a perfect square.
- Irrational Numbers: The square root of a number that is not a perfect square is an irrational number. This means its decimal representation goes on forever without repeating. The square root of 500 falls into this category.
- Approximation: Since we cannot express the square root of 500 exactly as a decimal, we rely on approximation techniques to find a close estimate.
Calculating the Square Root of 500: Different Approaches
Several methods exist for approximating the square root of 500. Let's explore some of the most common and effective approaches:
1. Using a Calculator
The simplest approach is using a calculator. Most calculators have a dedicated square root function (√). Simply enter 500 and press the square root button. The calculator will provide a decimal approximation, typically around 22.36067977.
2. Prime Factorization and Simplification
While 500 isn't a perfect square, we can simplify the radical expression using prime factorization. The prime factorization of 500 is 2² x 5³. This allows us to simplify the square root as follows:
√500 = √(2² x 5³) = √(2² x 5² x 5) = 2 x 5√5 = 10√5
This simplified form, 10√5, is an exact representation, but it still requires an approximation for √5. The approximate value of √5 is 2.236, so 10√5 ≈ 10 x 2.236 = 22.36.
3. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm for approximating square roots. It's a relatively simple method that converges quickly to the correct answer. The algorithm is as follows:
- Start with an initial guess: Let's guess 20.
- Improve the guess: Divide the number (500) by the guess (20) and average the result with the guess: (20 + 500/20) / 2 = 22.5
- Repeat step 2: Now use 22.5 as the new guess: (22.5 + 500/22.5) / 2 ≈ 22.361
- Iterate until desired accuracy: Continue this process until the difference between successive guesses is smaller than the desired level of accuracy.
This method demonstrates the iterative nature of approximating irrational numbers. Each iteration refines the approximation, converging towards the true value.
4. Linear Approximation
A simpler, albeit less accurate, method is linear approximation. We can use the known square roots of nearby perfect squares. We know that √484 = 22 and √529 = 23. Since 500 is closer to 484 than 529, we can make a rough estimate that √500 is slightly more than 22. This method provides a quick, but less precise, approximation.
5. Using a Spreadsheet or Programming Language
Spreadsheets like Microsoft Excel or Google Sheets, and programming languages like Python, offer built-in functions for calculating square roots. These tools are powerful for calculating the square root of 500 and performing more complex mathematical operations. For instance, in Excel, the formula =SQRT(500) would yield the same decimal approximation as a calculator.
Historical Context of Square Root Calculations
The calculation of square roots has a rich history, stretching back to ancient civilizations. The Babylonians developed sophisticated methods for approximating square roots, including the iterative technique discussed above (Heron's Method). The Greeks also contributed significantly to the understanding of irrational numbers and their properties. Over the centuries, mathematicians refined techniques and developed algorithms for increasingly accurate calculations. The invention of the calculator and computer significantly simplified the process, making accurate approximations readily accessible.
Applications of Square Roots
Square roots are not just abstract mathematical concepts; they have numerous applications in various fields:
- Physics: Square roots are essential in calculating velocity, acceleration, and other physical quantities. For example, the Pythagorean theorem (a² + b² = c²) heavily relies on square roots to determine the length of the hypotenuse of a right-angled triangle.
- Engineering: Square roots are used in structural calculations, electrical engineering, and many other engineering disciplines.
- Geometry: Numerous geometric calculations rely on square roots, such as finding the area of a triangle given its sides (Heron's formula) or calculating the diagonal of a square or rectangle.
- Statistics: Square roots appear in statistical calculations, such as standard deviation and variance.
- Computer Graphics: Square roots play a crucial role in computer graphics and 3D rendering, particularly in distance calculations and vector operations.
- Finance: Square roots are utilized in financial modeling, particularly in calculations related to portfolio optimization and risk management.
Conclusion
The square root of 500, while seemingly a simple question, provides a window into the fascinating world of mathematical approximation and computation. Various methods exist to determine its approximate value, from simple calculator use to more sophisticated iterative techniques. Understanding these methods not only provides a practical way to find the answer but also offers a deeper appreciation for the history and applications of square roots in various fields. The exploration of this seemingly simple mathematical problem unveils a wealth of mathematical concepts and their practical relevance in our world. The accuracy needed will depend entirely on the context of the problem; a rough estimate might suffice in some cases, while precise calculations are necessary in others.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.