What's The Square Root Of 54
News Co
Apr 07, 2025 · 5 min read
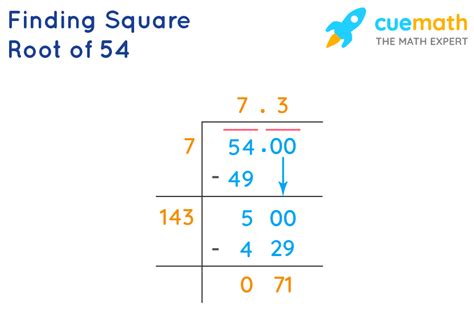
Table of Contents
What's the Square Root of 54? A Deep Dive into Square Roots and Approximations
The question, "What's the square root of 54?" seems simple enough. However, exploring this seemingly straightforward mathematical problem opens a door to a fascinating world of mathematical concepts, approximation techniques, and the beauty of irrational numbers. This article will delve into finding the square root of 54, exploring both the exact value and various methods for approximating it, and discussing the broader implications within mathematics.
Understanding Square Roots
Before diving into the specifics of the square root of 54, let's establish a foundational understanding of what a square root is. The square root of a number x is a value that, when multiplied by itself, equals x. In simpler terms, it's the number that, when squared, gives you the original number. For example, the square root of 9 (√9) is 3, because 3 * 3 = 9.
This concept extends to numbers that aren't perfect squares—numbers that don't have whole number square roots. 54 is one such number. Its square root is not a whole number; it's an irrational number. This means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Finding the Exact Value: The Irrationality of √54
Unlike the square root of a perfect square, the square root of 54 doesn't yield a neat, whole number answer. To find the exact value, we can simplify it using prime factorization.
54 can be factored as 2 × 3 × 3 × 3 = 2 × 3³. Therefore, √54 can be simplified as:
√54 = √(2 × 3³) = √(2 × 3² × 3) = √(3² × 2 × 3) = 3√(6)
This shows us the exact value of the square root of 54: 3√6. While this is precise, it doesn't give us a numerical value we can easily use in calculations. That's where approximation techniques come in.
Approximation Methods: Getting Closer to the Answer
Several methods exist to approximate the square root of 54. We'll explore some of the most common and effective ones:
1. Using a Calculator
The simplest and most straightforward method is to use a calculator. Most calculators have a square root function (√) that will directly give you an approximation of the square root. Using a calculator, we find that √54 ≈ 7.348469228.
2. The Babylonian Method (or Heron's Method)
This iterative method is an ancient algorithm for approximating square roots. It refines an initial guess through successive iterations, getting closer to the actual value with each step. Here's how it works:
-
Make an initial guess: Let's start with a guess of 7, as 7² = 49, which is close to 54.
-
Improve the guess: Divide the number (54) by the guess (7) and then average the result with the guess: (7 + 54/7) / 2 ≈ 7.357
-
Iterate: Repeat step 2, using the new approximation (7.357) as the guess: (7.357 + 54/7.357) / 2 ≈ 7.3485
-
Continue iterating: Continue this process until the desired level of accuracy is reached. Each iteration brings the approximation closer to the actual value.
3. Linear Approximation
This method uses the slope of the tangent line to the square root function at a nearby point. Let's consider the square root of 49 (which is 7). The derivative of √x is 1/(2√x). At x = 49, the derivative is 1/(2√49) = 1/14.
The linear approximation is then: √54 ≈ 7 + (1/14)(54 - 49) = 7 + (5/14) ≈ 7.357
This provides a reasonably accurate approximation, especially when compared to the true value.
4. Numerical Methods
More sophisticated numerical methods, such as the Newton-Raphson method, provide even more accurate approximations of square roots. These methods are often employed in computer programs and advanced calculators for high-precision calculations. They involve iterative processes that converge rapidly to the desired solution.
The Significance of Irrational Numbers
The fact that √54 is irrational highlights an important concept in mathematics. Irrational numbers are numbers that cannot be expressed as a fraction of two integers. They possess infinite, non-repeating decimal expansions. The existence of irrational numbers demonstrates the richness and complexity of the number system. They are fundamental to many areas of mathematics, including geometry and calculus.
Practical Applications
Understanding and approximating square roots has a wide range of practical applications in various fields:
-
Engineering and Physics: Calculating distances, areas, and volumes frequently involves square roots. For example, the Pythagorean theorem (a² + b² = c²) relies heavily on square roots to find the hypotenuse of a right-angled triangle.
-
Computer Graphics: Square roots are used in many computer graphics algorithms, particularly those related to transformations, rotations, and projections.
-
Statistics: Standard deviation, a key concept in statistics, involves calculating square roots.
-
Finance: Financial calculations often use square roots, such as in determining the present value of investments.
Conclusion: Beyond the Simple Question
The seemingly simple question, "What's the square root of 54?" has led us on a journey into the fascinating world of square roots, approximation methods, and irrational numbers. While we can't express √54 as a neat, whole number, we can find its exact value (3√6) and use various techniques to approximate it to any desired degree of accuracy. This exploration underscores the importance of understanding both the theoretical underpinnings and practical applications of mathematical concepts, even those that seem elementary at first glance. From ancient Babylonian methods to modern numerical analysis, the pursuit of precise calculations remains a cornerstone of mathematical inquiry and technological advancement. The journey of finding the square root of 54 is not just about a single number; it's a testament to the power and elegance of mathematics itself.
Latest Posts
Latest Posts
-
What Is The Square Root Of 43
Apr 08, 2025
-
What Number Is 10 Of 20
Apr 08, 2025
-
What Is 10 To The 23rd Power
Apr 08, 2025
-
How To Find The Nth Degree Polynomial Function
Apr 08, 2025
-
How Many Acres In A Square Mile Of Land
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.