What's The Square Root Of 55
News Co
Apr 06, 2025 · 5 min read
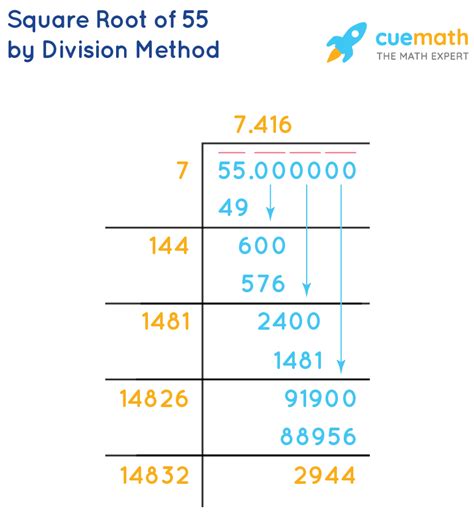
Table of Contents
What's the Square Root of 55? A Deep Dive into Irrational Numbers and Approximation Techniques
The seemingly simple question, "What's the square root of 55?" opens a fascinating window into the world of mathematics, specifically the realm of irrational numbers and numerical approximation methods. While a precise, finite decimal representation doesn't exist, understanding how to approach this problem reveals powerful mathematical concepts and practical techniques.
Understanding Square Roots and Irrational Numbers
Before diving into the specifics of the square root of 55, let's establish a foundational understanding. The square root of a number (√x) is a value that, when multiplied by itself, equals the original number (x). In simpler terms, it's the inverse operation of squaring a number.
55 is not a perfect square. A perfect square is a number that can be obtained by squaring a whole number (e.g., 9 is a perfect square because 3 x 3 = 9). Since there's no whole number that, when multiplied by itself, equals 55, the square root of 55 is an irrational number.
Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation is non-terminating (it goes on forever) and non-repeating (it doesn't have a repeating pattern). This means we can only approximate the value of √55.
Methods for Approximating √55
Several techniques allow us to find increasingly accurate approximations of the square root of 55. Let's explore some common and effective methods:
1. The Babylonian Method (or Heron's Method)
This iterative method refines an initial guess to progressively get closer to the actual square root. The formula is:
x<sub>n+1</sub> = ½ (x<sub>n</sub> + 55/x<sub>n</sub>)
where:
- x<sub>n</sub> is the current approximation
- x<sub>n+1</sub> is the next, improved approximation
Let's start with an initial guess of x<sub>0</sub> = 7 (because 7 x 7 = 49, which is close to 55):
- Iteration 1: x<sub>1</sub> = ½ (7 + 55/7) ≈ 7.357
- Iteration 2: x<sub>2</sub> = ½ (7.357 + 55/7.357) ≈ 7.416
- Iteration 3: x<sub>3</sub> = ½ (7.416 + 55/7.416) ≈ 7.416
As you can see, the method converges quickly. After just a few iterations, we obtain a highly accurate approximation of √55 ≈ 7.416.
2. Using a Calculator or Computer Software
Modern calculators and computer software programs have built-in functions to calculate square roots to a high degree of accuracy. Simply inputting "√55" will provide a result like 7.416198487... This method is the most convenient for practical purposes.
3. Linear Approximation
This simpler method uses the tangent line of the function f(x) = √x at a nearby perfect square. Since 49 (7²) is close to 55, we can use this approach:
- Find the derivative: The derivative of √x is 1/(2√x).
- Evaluate at x=49: 1/(2√49) = 1/14
- Linear approximation: √55 ≈ √49 + (1/14)(55-49) = 7 + (1/14)(6) ≈ 7.429
This method provides a less precise approximation than the Babylonian method, but it demonstrates a fundamental concept in calculus.
4. Newton-Raphson Method
Similar to the Babylonian method, the Newton-Raphson method is an iterative approach to finding successively better approximations of a function's root. The formula is:
x<sub>n+1</sub> = x<sub>n</sub> - f(x<sub>n</sub>) / f'(x<sub>n</sub>)
Where:
- f(x) = x² - 55 (we're looking for the root of this function)
- f'(x) = 2x (the derivative)
Starting with an initial guess, this method iteratively refines the approximation. The convergence speed is generally faster than the Babylonian method for many functions.
The Importance of Understanding Irrational Numbers
While we can approximate √55 to any desired degree of accuracy using computational methods, it's crucial to remember its irrational nature. This underscores the richness and complexity of the number system. Irrational numbers are fundamental to many areas of mathematics, including:
- Geometry: The diagonal of a unit square (√2) is an irrational number. Many geometric constructions involve irrational numbers.
- Trigonometry: Trigonometric functions often produce irrational results for certain angles.
- Calculus: Limits and derivatives frequently involve irrational numbers.
- Physics: Many physical constants, like π (pi) and e (Euler's number), are irrational.
Practical Applications and Beyond
The concept of finding square roots, even of seemingly simple numbers like 55, has far-reaching implications in various practical applications:
- Engineering: Calculating distances, areas, and volumes often requires working with square roots.
- Computer Graphics: Rendering 3D graphics relies heavily on calculations involving square roots for distance computations and perspective transformations.
- Physics: Many physics formulas involve square roots, for example, calculations related to projectile motion and energy.
- Finance: Calculating present and future values in financial models often uses square roots.
Conclusion: Embracing the Approximation
The quest to find the square root of 55 highlights the fascinating interplay between exact values and practical approximations. While we cannot express √55 as a finite decimal, understanding the different approximation methods allows us to obtain results accurate enough for most practical purposes. The journey to find this seemingly simple square root provides a valuable insight into the world of irrational numbers and strengthens our mathematical skills. The accuracy you need will depend on the application, but the methods outlined above provide a robust toolkit for tackling this and similar problems. Remember to choose the method that best suits your needs and desired level of precision. The beauty of mathematics lies in its ability to provide both elegant solutions and practical approximations, and understanding the nuances of both is essential for a well-rounded mathematical education.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 55 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.