What's The Square Root Of 61
News Co
Apr 01, 2025 · 5 min read
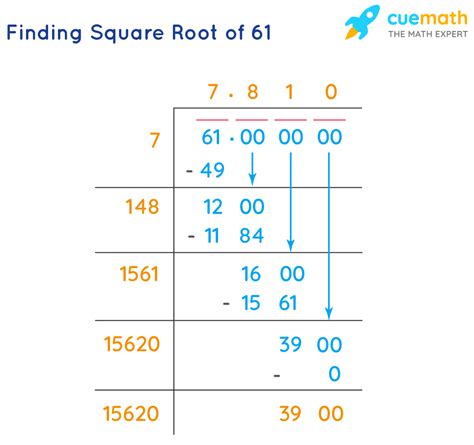
Table of Contents
What's the Square Root of 61? A Deep Dive into Irrational Numbers
The question, "What's the square root of 61?" seems simple enough. However, delving into this seemingly straightforward mathematical problem opens up a fascinating exploration of irrational numbers, numerical approximation techniques, and the beauty of mathematical precision. Let's embark on this journey together.
Understanding Square Roots
Before we tackle the specific case of the square root of 61, let's establish a fundamental understanding of square roots. The square root of a number (x) is a value (y) that, when multiplied by itself, equals x. In simpler terms: y * y = x, or y² = x. Therefore, the square root of x is denoted as √x or x<sup>1/2</sup>.
For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
- √25 = 5 because 5 * 5 = 25
These are perfect squares – numbers that have whole number square roots. However, many numbers don't have such neat whole number solutions. This brings us to the fascinating world of irrational numbers.
Irrational Numbers: The Nature of √61
The square root of 61 (√61) falls into the category of irrational numbers. Irrational numbers are numbers that cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representations are non-terminating and non-repeating, meaning they go on forever without ever settling into a repeating pattern. This is in contrast to rational numbers, which can be expressed as a fraction and have either terminating or repeating decimal expansions.
This inherent characteristic of √61 makes finding its exact value impossible. We can only approximate its value to a certain degree of accuracy. This lack of a precise, finite representation is a key aspect of understanding irrational numbers and their importance in mathematics.
Methods for Approximating √61
Several methods exist for approximating the square root of 61. Let's explore some of the most common approaches:
1. Using a Calculator
The simplest method is using a calculator. Most scientific calculators have a dedicated square root function (√). Inputting 61 and pressing the square root button will provide a decimal approximation. Calculators typically provide a high degree of precision, often displaying several decimal places. For √61, a calculator might yield something like 7.8102496759. However, remember that this is still an approximation, not the true, exact value.
2. The Babylonian Method (Heron's Method)
This iterative method is an ancient algorithm for approximating square roots. It involves repeatedly refining an initial guess until the desired level of accuracy is achieved. Here's how it works:
- Start with an initial guess: Let's choose 8 as our initial guess because 8² = 64, which is close to 61.
- Improve the guess: Divide 61 by the initial guess (61/8 ≈ 7.625).
- Average the results: Average the initial guess and the result from step 2: (8 + 7.625)/2 ≈ 7.8125.
- Repeat steps 2 and 3: Use the new average as the next guess and repeat the process until the desired level of accuracy is reached.
By iterating this method, you can achieve increasingly accurate approximations of √61. Each iteration brings the approximation closer to the true value. This method demonstrates a practical approach to approximating square roots without relying on advanced calculators.
3. Linear Approximation
Linear approximation leverages the tangent line of a function at a known point to estimate the function's value at a nearby point. In this case, we can consider the function f(x) = √x and approximate √61 using the value of √64 (which is 8). The derivative of f(x) = √x is f'(x) = 1/(2√x). Using the tangent line approximation:
√61 ≈ √64 + f'(64) * (61 - 64) = 8 + (1/(2√64)) * (-3) = 8 - 3/16 ≈ 7.8125
This method, while less precise than the Babylonian method after multiple iterations, provides a quick estimate using basic calculus.
4. Using Continued Fractions
Continued fractions offer another method for approximating irrational numbers. Expressing √61 as a continued fraction involves a sequence of integers and fractions. While the derivation is beyond the scope of this article, the resulting continued fraction provides a series of increasingly accurate rational approximations of √61.
The Significance of Irrational Numbers
The existence of irrational numbers like √61 highlights the richness and complexity of the number system. While we can only approximate their values, their theoretical importance is immense. They play a crucial role in various mathematical fields, including:
- Geometry: Irrational numbers are frequently encountered in geometric calculations, particularly those involving circles and triangles. The famous constant π (pi), which represents the ratio of a circle's circumference to its diameter, is an irrational number.
- Calculus: Irrational numbers are essential in calculus, where they often appear as limits and solutions to equations.
- Trigonometry: Many trigonometric functions involve irrational numbers, reflecting the inherent relationships between angles and lengths in geometric figures.
Practical Applications of √61 Approximation
While the square root of 61 might seem like a purely theoretical concept, approximations of irrational numbers find practical applications in diverse fields:
- Engineering: Calculations in structural engineering, electrical engineering, and other fields often involve approximations of irrational numbers to design and build structures and systems. The precision required depends on the application; sometimes a rough estimate suffices, while other situations demand higher accuracy.
- Physics: Many physics calculations, particularly those dealing with motion, waves, and energy, involve irrational numbers, requiring accurate approximations for precise predictions and simulations.
- Computer Graphics: Rendering realistic images in computer graphics necessitates the use of accurate approximations of irrational numbers for smooth curves and shapes.
Conclusion: Embracing the Approximation
The quest to find the square root of 61 leads us to appreciate the nature of irrational numbers and the elegance of various approximation methods. While we cannot express √61 as a simple fraction or a terminating decimal, we can obtain approximations to any desired level of accuracy using methods like the Babylonian method, linear approximation, or calculators. Understanding the limitations and power of these approximations is crucial for practical applications across various fields, solidifying the importance of irrational numbers in the fabric of mathematics and its diverse applications in the real world. Remember, the beauty lies not in finding the perfect answer (which is impossible in this case), but in understanding the process and the profound implications of exploring such mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 61 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.