What's The Square Root Of 63
News Co
Apr 07, 2025 · 5 min read
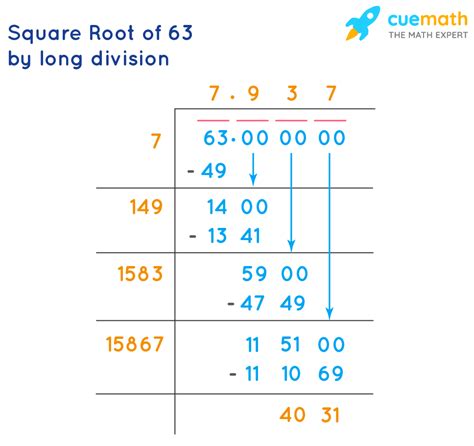
Table of Contents
What's the Square Root of 63? A Deep Dive into Square Roots and Approximation Techniques
The seemingly simple question, "What's the square root of 63?" opens a door to a fascinating exploration of mathematical concepts, approximation techniques, and the power of computational tools. While a simple calculator will provide a decimal approximation, understanding the underlying principles enriches our mathematical understanding. This article will delve into the intricacies of square roots, specifically focusing on the square root of 63, and explore various methods for finding its value.
Understanding Square Roots
Before we tackle the square root of 63, let's establish a firm understanding of what a square root represents. The square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example, the square root of 9 is 3 because 3 x 3 = 9. This can be mathematically represented as:
√x = y if and only if y² = x
Where 'x' is the number and 'y' is its square root.
Finding the Square Root of 63: The Challenges
Unlike perfect squares like 9, 16, or 25, 63 isn't a perfect square. This means its square root is not a whole number. This presents a challenge: we need to use approximation methods or computational tools to find its value. This inherent challenge makes understanding the various approaches all the more rewarding.
Methods for Approximating √63
Several methods can help us approximate the square root of 63. Let's examine a few:
1. Estimation through Perfect Squares
We can start by identifying perfect squares close to 63. We know that 8² = 64 and 7² = 49. Since 63 lies between 49 and 64, we can deduce that the square root of 63 must be between 7 and 8. This gives us a rough estimate, but we can refine it further. Because 63 is closer to 64 than 49, we can reasonably guess that the square root of 63 is slightly less than 8, perhaps around 7.9.
2. Babylonian Method (Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm for approximating square roots. It refines an initial guess through successive calculations. The formula is:
x_(n+1) = 0.5 * (x_n + (N / x_n))
Where:
- x_n is the current approximation
- x_(n+1) is the next approximation
- N is the number whose square root we're seeking (in our case, 63)
Let's apply this method, starting with our initial estimate of 8:
- Iteration 1: x_1 = 0.5 * (8 + (63 / 8)) ≈ 7.9375
- Iteration 2: x_2 = 0.5 * (7.9375 + (63 / 7.9375)) ≈ 7.93725
Notice how quickly the approximation converges. Further iterations would yield even more precise results.
3. Using a Calculator or Computer
The most straightforward method is to use a calculator or computer software. These tools employ sophisticated algorithms to calculate square roots with high precision. Using a calculator, we find that:
√63 ≈ 7.93725393319
This value is accurate to several decimal places.
Beyond the Calculation: Understanding the Significance
While obtaining the numerical value of √63 is important, it's equally crucial to understand the context and implications of square roots in mathematics and various fields.
Square Roots in Geometry
Square roots frequently appear in geometrical calculations. For example, finding the length of the diagonal of a square with side length 'a' involves the Pythagorean theorem: diagonal = a√2. Similarly, calculating the distance between two points in a coordinate system often requires computing square roots.
Square Roots in Physics
Many physics formulas incorporate square roots. For instance, calculating the velocity of an object in free fall involves the square root of distance and acceleration due to gravity.
Square Roots in Statistics
Standard deviation, a key concept in statistics representing data dispersion, involves calculating the square root of variance.
Practical Applications: Real-World Examples
Understanding square roots isn't confined to theoretical mathematics. Consider the following practical applications:
-
Construction and Engineering: Calculating the length of diagonals, determining the area of irregular shapes, and structural design often utilize square roots.
-
Computer Graphics: Rendering 3D graphics and animations extensively uses square roots for distance calculations, transformations, and other geometric operations.
-
Financial Modeling: Calculating compound interest and other financial parameters often involves the use of square roots.
Expanding our Knowledge: Related Concepts
Understanding square roots opens the door to related mathematical concepts, such as:
-
Cube roots: Similar to square roots, but involve finding a number that, when multiplied by itself three times, equals the original number.
-
Higher-order roots: Generalizing the concept of square and cube roots to any positive integer power.
-
Radical expressions: Mathematical expressions involving square roots and other radicals.
-
Irrational numbers: Numbers that cannot be expressed as a fraction of two integers (like the square root of 63).
Conclusion: More Than Just a Number
The seemingly straightforward question of finding the square root of 63 leads us on a journey through mathematical concepts, approximation techniques, and real-world applications. It highlights the importance of understanding not just the numerical answer but also the underlying principles and broader implications. From simple estimations to sophisticated algorithms, this exploration demonstrates the diverse methods available for approximating irrational numbers and emphasizes the power of mathematical tools in solving real-world problems. The quest to find the square root of 63 becomes a journey of mathematical discovery, showcasing the elegance and practical utility of this fundamental concept. The approximate value, roughly 7.937, is just the beginning of a deeper understanding of mathematics and its pervasive influence on our lives.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.