What's The Square Root Of 96
News Co
Apr 03, 2025 · 4 min read
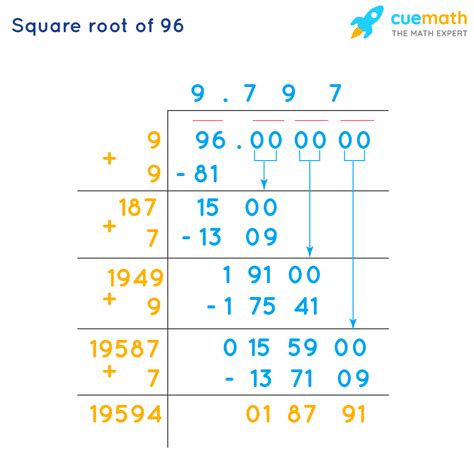
Table of Contents
What's the Square Root of 96? A Deep Dive into Square Roots and Approximation Techniques
The seemingly simple question, "What's the square root of 96?", opens a door to a fascinating world of mathematical concepts and techniques. While a calculator readily provides the decimal approximation, understanding the underlying principles and methods for calculating square roots offers a deeper appreciation of mathematics. This article explores various approaches to finding the square root of 96, from estimation and approximation methods to utilizing calculators and understanding the nature of irrational numbers.
Understanding Square Roots
Before delving into the specifics of finding the square root of 96, let's establish a foundational understanding of what a square root actually is. The square root of a number is a value that, when multiplied by itself (squared), gives the original number. For example, the square root of 25 is 5 because 5 * 5 = 25.
Mathematically, we represent the square root using the radical symbol (√). Therefore, the square root of 96 is written as √96.
Estimating the Square Root of 96
Before resorting to calculators or complex algorithms, let's try to estimate the value of √96. We can do this by identifying perfect squares close to 96.
-
Perfect squares: We know that 9² = 81 and 10² = 100. Since 96 lies between 81 and 100, we can deduce that √96 must be between 9 and 10.
-
Refining the estimate: 96 is closer to 100 than to 81. Therefore, we can anticipate that √96 is closer to 10 than to 9. A reasonable initial estimate might be around 9.8.
This estimation provides a good starting point, and we can refine it using more advanced techniques, as we will explore later.
The Babylonian Method (or Heron's Method)
The Babylonian method, also known as Heron's method, is an iterative algorithm for approximating square roots. It's a remarkably efficient method that converges quickly to the correct answer. Here's how it works:
-
Initial guess: Start with an initial guess for the square root. Our initial estimate of 9.8 is a good starting point.
-
Iteration: Apply the following formula repeatedly:
x_(n+1) = 0.5 * (x_n + (N / x_n))Where:
x_nis the current guess.x_(n+1)is the next, improved guess.Nis the number whose square root we're seeking (in this case, 96).
-
Iteration: Repeat step 2 until the desired level of accuracy is achieved. The difference between successive guesses will become smaller with each iteration.
Let's perform a few iterations:
-
Iteration 1:
x_1 = 0.5 * (9.8 + (96 / 9.8)) ≈ 9.797959 -
Iteration 2:
x_2 = 0.5 * (9.797959 + (96 / 9.797959)) ≈ 9.79795897
Notice how quickly the value converges. After just two iterations, we have a very accurate approximation of √96.
Prime Factorization Method
Another approach involves prime factorization. This method is particularly useful when dealing with perfect squares or numbers with easily identifiable factors. While 96 is not a perfect square, prime factorization can still be helpful in simplifying the expression.
The prime factorization of 96 is 2<sup>5</sup> * 3. We can rewrite √96 as:
√96 = √(2<sup>5</sup> * 3) = √(2<sup>4</sup> * 2 * 3) = √(2<sup>4</sup>) * √(2 * 3) = 4√6
This simplifies the square root to 4√6. We can then use a calculator or approximation methods to find the approximate value of √6 and multiply it by 4.
Using a Calculator
The simplest way to find the square root of 96 is to use a calculator. Most calculators have a dedicated square root function (√). Simply enter 96 and press the square root button. The calculator will provide a decimal approximation, typically around 9.79795897.
The Nature of √96: Irrational Numbers
It's important to note that √96 is an irrational number. Irrational numbers cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation is non-terminating and non-repeating. This means the decimal approximation of √96 will go on forever without a repeating pattern.
Application of Square Roots
Understanding square roots has numerous applications across various fields:
- Geometry: Calculating distances, areas, and volumes often involves square roots (e.g., the Pythagorean theorem).
- Physics: Many physical phenomena, such as velocity, acceleration, and energy calculations, utilize square roots.
- Engineering: Square roots are essential in various engineering calculations, including structural analysis and electrical circuit design.
- Finance: Compound interest calculations and other financial models often involve square roots.
- Computer Graphics: Square roots are used extensively in computer graphics for transformations, rotations, and 3D rendering.
Conclusion: More Than Just a Number
The seemingly simple question of finding the square root of 96 opens the door to a rich understanding of mathematical concepts and techniques. From estimation and approximation methods like the Babylonian method to prime factorization and the use of calculators, there are various approaches to arrive at the answer. Moreover, understanding the nature of irrational numbers and the wide applicability of square roots in various fields enriches our mathematical literacy. Therefore, the next time you encounter a square root problem, remember that there's more than just a numerical answer waiting to be discovered – there's a whole world of mathematical exploration at your fingertips. Remember to practice different techniques to strengthen your mathematical skills and understanding. The more you engage with these concepts, the easier and more intuitive they become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 96 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.