Which Expression Is Equivalent To 4 7i 3 4i
News Co
Mar 19, 2025 · 5 min read
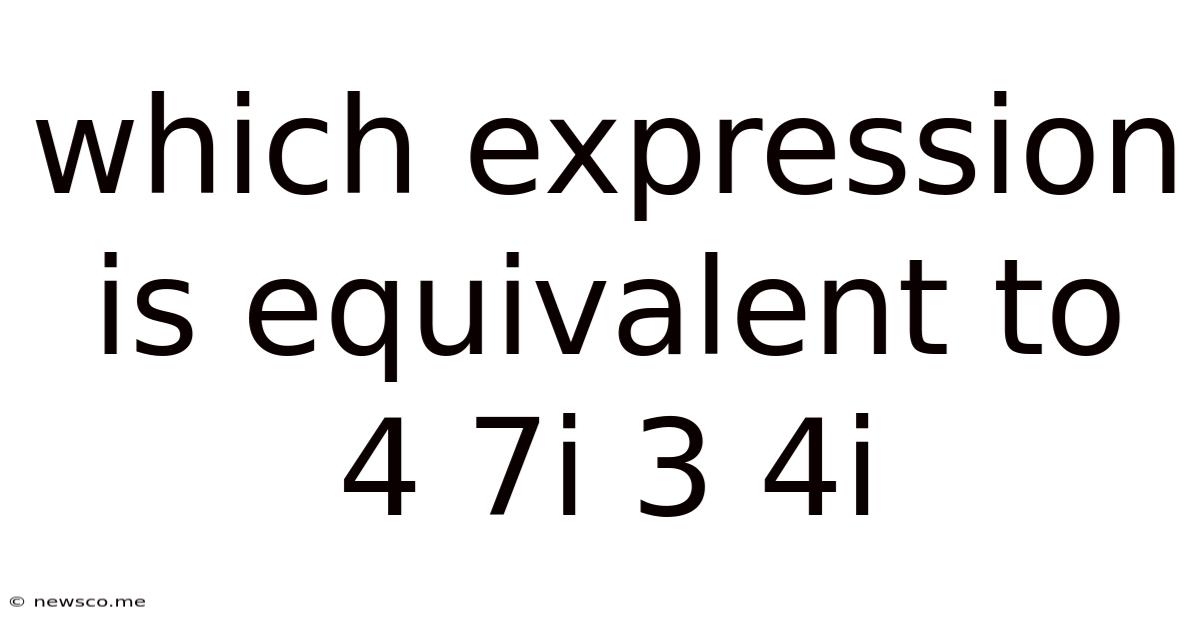
Table of Contents
Which Expression is Equivalent to 4 + 7i + 3 + 4i? A Deep Dive into Complex Number Simplification
This article explores the simplification of the complex number expression 4 + 7i + 3 + 4i, providing a comprehensive understanding of the process and its underlying principles. We'll delve into the basics of complex numbers, demonstrating various methods for simplification and highlighting the importance of understanding complex number arithmetic for various applications in mathematics, engineering, and physics.
Understanding Complex Numbers
Before tackling the simplification, let's briefly revisit the definition of complex numbers. A complex number is a number that can be expressed in the form a + bi, where:
- a is the real part of the complex number.
- b is the imaginary part of the complex number.
- i is the imaginary unit, defined as the square root of -1 (√-1).
Complex numbers extend the concept of real numbers by incorporating the imaginary unit, allowing for the representation and manipulation of numbers that aren't solely located on the number line. They are crucial in solving equations that have no real number solutions.
Simplifying 4 + 7i + 3 + 4i
The expression 4 + 7i + 3 + 4i involves the addition of two complex numbers. The process of simplification relies on the fundamental principles of combining like terms. In complex numbers, this means combining the real parts and the imaginary parts separately.
Step-by-Step Simplification:
-
Group the real parts: We have the real numbers 4 and 3.
-
Group the imaginary parts: We have the imaginary numbers 7i and 4i.
-
Combine the real parts: 4 + 3 = 7
-
Combine the imaginary parts: 7i + 4i = 11i
-
Combine the simplified real and imaginary parts: 7 + 11i
Therefore, the simplified expression equivalent to 4 + 7i + 3 + 4i is 7 + 11i.
Alternative Approaches and Visual Representation
While the above method is the most straightforward, let's explore alternative ways to visualize and approach this problem.
1. Using Vector Representation:
Complex numbers can be represented graphically as vectors in the complex plane (also known as the Argand plane). The real part represents the horizontal component, and the imaginary part represents the vertical component. Adding complex numbers graphically involves vector addition. If we represent 4 + 7i and 3 + 4i as vectors, their sum would be the resultant vector representing 7 + 11i. This visual approach reinforces the concept of adding the real and imaginary parts independently.
2. Applying the Distributive Property (though not strictly necessary here):
While not essential for this particular problem, the distributive property can be applied in more complex scenarios involving multiplication or factoring of complex numbers. This property, a(b + c) = ab + ac, ensures consistency and accuracy in calculations. In this case, it wouldn't directly simplify the addition, but it’s a crucial tool in other complex number manipulations.
Importance and Applications of Complex Number Simplification
The ability to simplify complex number expressions is fundamental to numerous applications in various fields:
-
Electrical Engineering: Complex numbers are crucial in analyzing alternating current (AC) circuits. Impedance, a measure of opposition to current flow, is often expressed as a complex number. Simplifying complex expressions allows for efficient calculations of circuit parameters.
-
Signal Processing: Complex numbers are widely used in representing and manipulating signals. The Fourier transform, a cornerstone of signal processing, utilizes complex numbers to decompose signals into their frequency components. Simplification of complex expressions improves computational efficiency and accuracy in signal analysis.
-
Quantum Mechanics: Complex numbers are integral to the mathematical framework of quantum mechanics. Wave functions, which describe the state of a quantum system, are often complex-valued. Simplifying complex expressions is critical for calculations and interpretations within quantum mechanics.
-
Fluid Dynamics: Complex analysis is used in solving certain fluid flow problems. Complex potential functions describe aspects of fluid motion, requiring manipulation of complex expressions for accurate analysis.
-
Control Systems: Complex numbers are used in the analysis and design of control systems. The transfer function, which describes the relationship between the input and output of a system, is often a complex function. Simplification of complex expressions is essential for understanding and manipulating system behavior.
Further Exploration: More Complex Scenarios
While this example focused on a simple addition of two complex numbers, the principles of combining like terms remain consistent for more complex expressions involving subtraction, multiplication, division, and powers of complex numbers.
Subtraction: Subtracting complex numbers involves subtracting the real parts and the imaginary parts separately. For example, (4 + 7i) - (3 + 4i) = (4 - 3) + (7i - 4i) = 1 + 3i.
Multiplication: Multiplication of complex numbers involves the distributive property and the fact that i² = -1. For instance, (2 + 3i)(1 + 2i) = 2 + 4i + 3i + 6i² = 2 + 7i - 6 = -4 + 7i.
Division: Division of complex numbers involves multiplying both the numerator and denominator by the complex conjugate of the denominator. The complex conjugate of a + bi is a - bi. This process eliminates the imaginary part from the denominator, simplifying the expression.
Powers: Raising a complex number to a power involves using De Moivre's theorem, which relates the powers of complex numbers to their polar form (magnitude and angle).
Conclusion:
The simplification of the expression 4 + 7i + 3 + 4i to 7 + 11i demonstrates a fundamental concept in complex number arithmetic – the combination of like terms. This seemingly simple procedure forms the basis for more advanced calculations in various fields. Mastering this skill is crucial for anyone working with complex numbers in mathematics, engineering, physics, or computer science. Understanding the visual representation through vector addition further solidifies the concept and lays the groundwork for more complex computations involving multiple complex numbers and different operations. The ability to efficiently simplify these expressions is a cornerstone of successfully applying complex numbers to solve real-world problems.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 4 7i 3 4i . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.