Which Expression Is Equivalent To 4x 5 11 2
News Co
May 02, 2025 · 5 min read
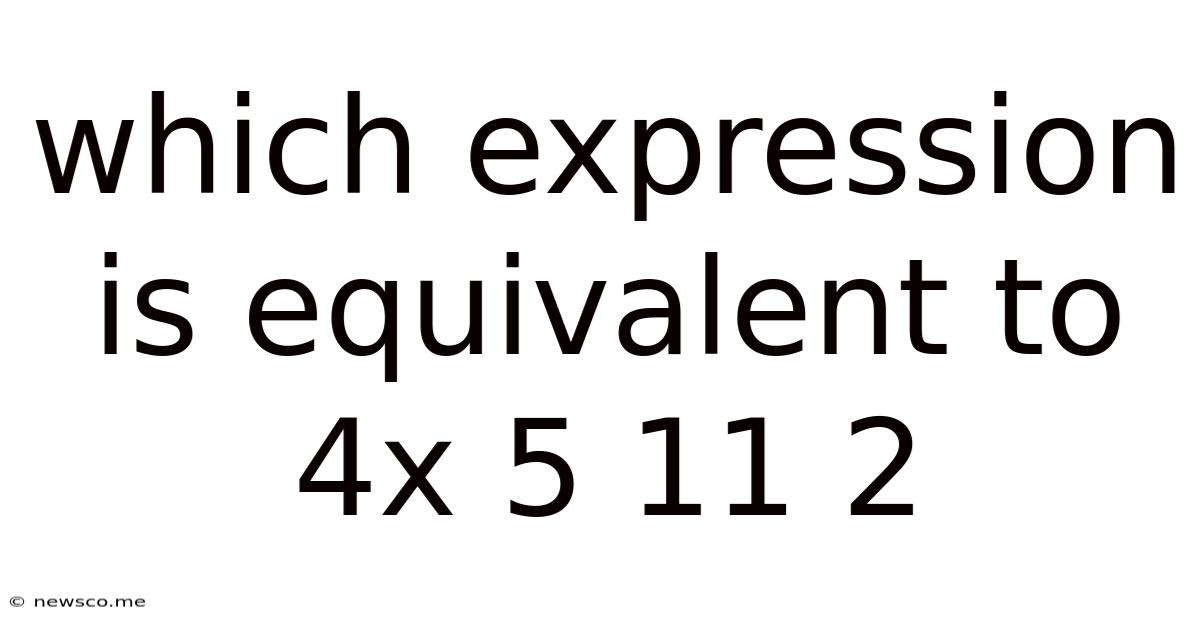
Table of Contents
Which Expression is Equivalent to 4x + 5 = 11 - 2? Solving Linear Equations and Equivalent Expressions
This article will delve into the process of determining which expression is equivalent to 4x + 5 = 11 - 2. We'll explore the fundamental principles of solving linear equations, identify equivalent expressions, and discuss practical applications. Understanding equivalent expressions is crucial for simplifying equations, solving for unknown variables, and ultimately, mastering algebra.
Understanding Equivalent Expressions
Before we tackle the specific equation, let's clarify the concept of equivalent expressions. Equivalent expressions are mathematical phrases that, despite looking different, produce the same result when evaluated for any given value of the variable(s). They are essentially different ways of representing the same mathematical relationship.
For instance, 2x + 6 and 2(x + 3) are equivalent expressions. No matter what value you substitute for 'x', both expressions will always yield the same numerical answer. This equivalence is established through the application of algebraic properties like the distributive property, combining like terms, and other simplification techniques.
Solving the Equation: 4x + 5 = 11 - 2
The equation presented, 4x + 5 = 11 - 2, is a linear equation. Linear equations are equations where the highest power of the variable (in this case, 'x') is 1. Solving such equations involves isolating the variable to find its value.
Let's break down the process step-by-step:
1. Simplify the Right-Hand Side (RHS):
The first step is to simplify the right-hand side of the equation. 11 - 2 simplifies to 9. Therefore, our equation becomes:
4x + 5 = 9
2. Isolate the Term with the Variable:
Our goal is to isolate the term containing 'x', which is 4x. To do this, we need to eliminate the constant term, '+5', from the left-hand side (LHS). We can achieve this by subtracting 5 from both sides of the equation. This maintains the equation's balance, as any operation performed on one side must also be performed on the other.
4x + 5 - 5 = 9 - 5
This simplifies to:
4x = 4
3. Solve for the Variable:
Now, we have 4x = 4. To solve for 'x', we need to divide both sides of the equation by the coefficient of 'x', which is 4.
4x / 4 = 4 / 4
This gives us:
x = 1
Therefore, the solution to the equation 4x + 5 = 11 - 2 is x = 1.
Identifying Equivalent Expressions: Context is Key
The question "Which expression is equivalent to 4x + 5 = 11 - 2?" requires careful interpretation. The original statement isn't asking for an equivalent expression for the whole equation, but rather an equivalent expression that represents the same solution or relationship as the equation. This distinction is vital.
To find equivalent expressions, we can manipulate the original equation using algebraic properties. For example:
-
Subtracting 5 from both sides:
4x = 9 - 5simplifies to4x = 4. This is an equivalent expression because it represents the same solution. -
Dividing both sides by 4:
x = 4 / 4simplifies tox = 1. This is another equivalent expression, representing the final solution. -
Starting with the solution:
x = 1itself can be considered an equivalent representation, though it’s the most simplified form.
These expressions, while visually different, are all equivalent in the context of representing the solution to the original linear equation. Any expression that eventually leads to x = 1 when simplified could be considered equivalent. Note that expressions like 2x + 2 or x + x are not equivalent to the original equation itself, as they don't incorporate the constant values. They represent different mathematical relationships.
Practical Applications and Extensions
Understanding equivalent expressions and solving linear equations is fundamental to various aspects of mathematics and beyond. Here are a few examples:
-
Physics: Many physics problems involve setting up and solving linear equations to determine unknowns like velocity, acceleration, or force. Understanding equivalent expressions allows for simplification and efficient problem-solving.
-
Engineering: Engineering design often requires solving systems of linear equations to analyze structural stability, circuit behavior, or fluid dynamics.
-
Finance: Calculating compound interest, analyzing investment returns, or projecting financial growth often involves using linear equations and the manipulation of equivalent expressions.
-
Computer Science: Linear equations are frequently used in computer graphics, algorithms, and data analysis.
-
Everyday Life: Simple scenarios, such as calculating the total cost of items with discounts, involve using basic linear equations.
Advanced Concepts and Further Exploration
While the original equation is straightforward, this concept extends to more complex scenarios:
-
Systems of Linear Equations: Instead of one equation, you might have multiple equations with multiple variables. Solving such systems requires techniques like substitution, elimination, or matrix methods. Equivalent expressions are still crucial for simplifying the equations and finding solutions.
-
Quadratic Equations: These equations involve variables raised to the power of 2. While solving them differs from linear equations (requiring methods like factoring or the quadratic formula), the concept of equivalent expressions remains essential for simplification and manipulation.
-
Inequalities: Instead of an equals sign, inequalities use symbols like <, >, ≤, and ≥. Solving inequalities involves similar techniques to solving equations, but with important considerations regarding the direction of the inequality sign when multiplying or dividing by a negative number. Equivalent expressions still play a vital role in simplifying inequalities.
Conclusion
Determining which expression is equivalent to 4x + 5 = 11 - 2 involves not just solving the equation but also understanding the concept of equivalence itself. While multiple expressions may represent the same solution (x = 1), it’s critical to recognize that only those expressions derived through proper algebraic manipulation are truly equivalent. Mastering this concept is fundamental to building a solid foundation in algebra and its numerous practical applications. The skill of manipulating and simplifying expressions paves the way for tackling more complex mathematical problems across various disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 4x 5 11 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.