Which Expression Is Equivalent To 5 2 5 1
News Co
May 07, 2025 · 5 min read
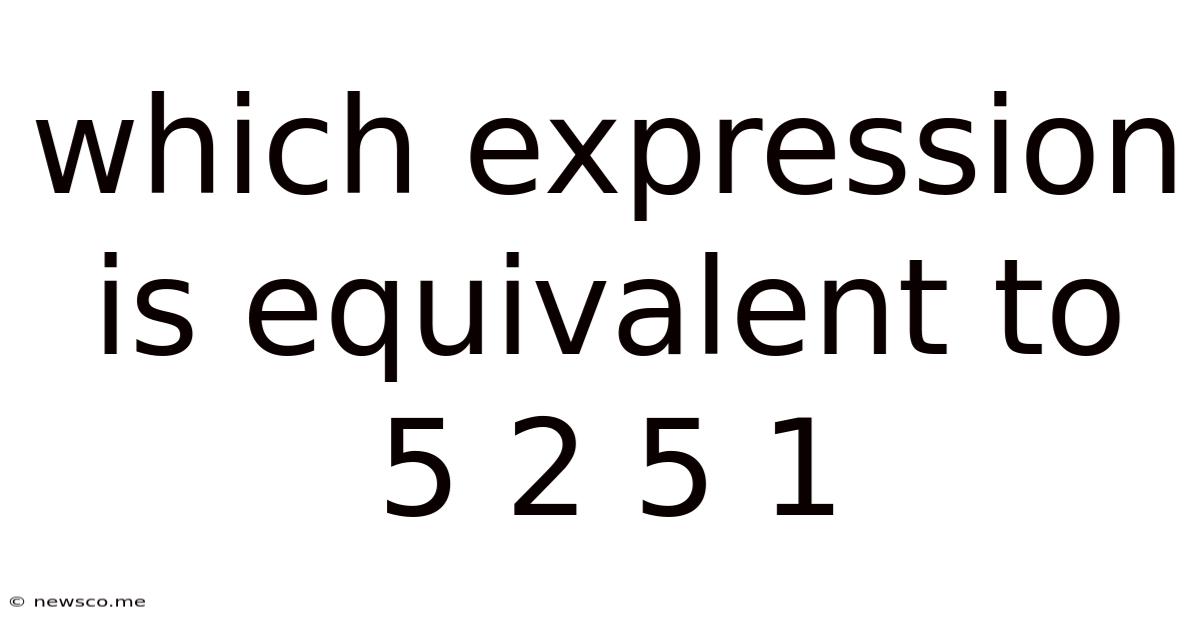
Table of Contents
Which Expression is Equivalent to 5² 5¹? A Deep Dive into Mathematical Equivalence
The seemingly simple question, "Which expression is equivalent to 5² 5¹?", opens a door to a deeper understanding of mathematical operations, particularly exponents and their properties. While the answer might seem immediately obvious to some, exploring the nuances of this question allows us to solidify our grasp of fundamental algebraic concepts and lays the groundwork for tackling more complex mathematical problems. This article will not only answer the question but will also explore the underlying principles, provide various equivalent expressions, and discuss the broader implications of understanding mathematical equivalence.
Understanding Exponents and Their Properties
Before diving into the specific problem, let's establish a solid foundation by reviewing the concept of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example:
- 5² means 5 multiplied by itself twice: 5 x 5 = 25
- 5¹ means 5 multiplied by itself once (or simply 5).
The core principle governing operations with exponents lies in their properties. These properties allow us to manipulate and simplify expressions containing exponents. Crucially for this problem, we'll focus on the product of powers property:
a<sup>m</sup> * a<sup>n</sup> = a<sup>(m+n)</sup>
This property states that when multiplying two terms with the same base, we can add their exponents. This is the key to finding equivalent expressions for 5² 5¹.
Solving the Equation: Finding Equivalent Expressions for 5² 5¹
Now, let's apply the product of powers property to our problem: 5² 5¹. Both terms share the same base (5). Therefore, we can add the exponents:
5² 5¹ = 5<sup>(2+1)</sup> = 5³
Therefore, 5³ is an equivalent expression to 5² 5¹. This simplifies to 5 x 5 x 5 = 125. So, any expression that evaluates to 125 is also equivalent.
Exploring Further Equivalent Expressions
While 5³ is the most straightforward equivalent expression, we can explore other possibilities by employing different mathematical operations and properties. Here are a few examples:
-
125: This is the simplest form, representing the numerical result of the calculation. It's an equivalent expression, though not as insightful in terms of mathematical structure.
-
(5 x 5) x 5: This expression explicitly demonstrates the repeated multiplication inherent in the exponent 3.
-
5 x 25: This showcases the intermediate step of calculating 5² before multiplying by 5.
-
(100 + 25) / 4 + 100: This is a more complex example, showing how 125 can be constructed using a variety of arithmetic operations. The goal here is to highlight the various ways numbers can be manipulated to result in the same value. This is especially important when dealing with more complicated equations.
-
√(15625): This illustrates that even root operations can be used, as the square root of 15625 (125 squared) equals 125.
These examples demonstrate that equivalent expressions can take many forms, highlighting the flexibility and power of mathematical manipulation. The key is that, regardless of the form, all these expressions ultimately evaluate to the same numerical value: 125.
The Significance of Understanding Mathematical Equivalence
The ability to identify and manipulate equivalent expressions is fundamental to success in mathematics and related fields. This skill enables us to:
-
Simplify complex expressions: By recognizing equivalent expressions, we can simplify complex mathematical expressions into more manageable forms, making calculations easier and more efficient. This is crucial in solving more intricate problems.
-
Solve equations: Finding equivalent expressions is essential for solving equations. Manipulating equations using equivalent expressions allows us to isolate variables and find solutions.
-
Improve problem-solving skills: Understanding mathematical equivalence fosters a deeper understanding of the relationships between different mathematical constructs. This enhances problem-solving skills, allowing for creative solutions and a broader perspective.
-
Enhance understanding of mathematical properties: The process of finding equivalent expressions reinforces our understanding of fundamental mathematical properties like the commutative, associative, and distributive properties, as well as the properties of exponents.
Applications in Real-World Scenarios
The concept of mathematical equivalence isn't confined to theoretical mathematical problems; it has practical applications in many fields:
-
Computer Science: In programming and software development, understanding equivalent expressions is crucial for optimizing algorithms and code efficiency. Equivalent expressions can lead to significantly different performance levels.
-
Engineering: Engineers frequently use equivalent expressions to simplify complex calculations and ensure the accuracy of their designs. Whether it's structural analysis, circuit design, or fluid dynamics, manipulating equations to create simpler equivalent expressions is crucial for efficient and effective problem-solving.
-
Finance: In financial modeling and investment analysis, understanding equivalent expressions is crucial for accurate calculations of interest, returns, and risk assessments. Manipulating financial formulas using equivalent expressions improves the clarity and efficiency of these calculations.
-
Physics: Many physical laws and formulas are expressed using mathematical equations. Using equivalent expressions allows physicists to simplify these equations and derive new insights into physical phenomena.
Conclusion: Beyond the Simple Answer
The answer to the question, "Which expression is equivalent to 5² 5¹?", is undeniably 5³. However, the true value of exploring this question lies in understanding the underlying principles and their broader implications. By delving into the properties of exponents and the concept of mathematical equivalence, we gain a more profound understanding of mathematical operations and their applications in various fields. The ability to recognize and manipulate equivalent expressions is a cornerstone of mathematical proficiency, paving the way for tackling more complex challenges and contributing to problem-solving skills in various disciplines. The seemingly simple equation is, therefore, a gateway to a much richer and more profound understanding of mathematics and its relevance in the real world. This article serves as a stepping stone to further explore the fascinating world of mathematical equivalence and its applications. Remember to always explore different approaches and methods to solidify your understanding and to appreciate the beauty and power of mathematical principles.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Which Expression Is Equivalent To 5 2 5 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.