Which Fraction Is Equivalent To 1 4
News Co
Apr 06, 2025 · 5 min read
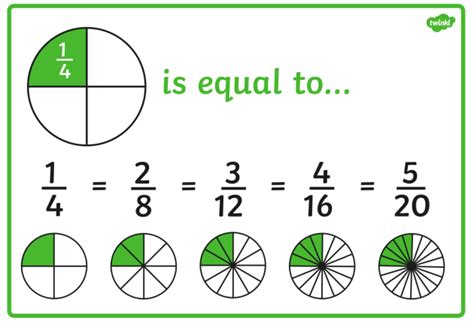
Table of Contents
Which Fraction is Equivalent to 1 ¼? Understanding Equivalent Fractions
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding operations with fractions, simplifying expressions, and solving various mathematical problems. This article delves deep into the concept of equivalent fractions, focusing specifically on finding fractions equivalent to the mixed number 1 ¼. We will explore different methods, provide numerous examples, and explain the underlying principles to solidify your understanding.
What are Equivalent Fractions?
Equivalent fractions represent the same portion or value, even though they appear different. Imagine slicing a pizza: one-half (½) is the same as two-quarters (²/₄) or three-sixths (³/₆). These fractions all represent exactly half of the pizza. The key is that the ratio between the numerator (the top number) and the denominator (the bottom number) remains constant. You can obtain an equivalent fraction by multiplying or dividing both the numerator and denominator by the same non-zero number.
Converting Mixed Numbers to Improper Fractions
The mixed number 1 ¼ represents one whole unit and one-quarter of a unit. Before we find equivalent fractions, it's helpful to convert this mixed number into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
To convert 1 ¼ to an improper fraction:
- Multiply the whole number by the denominator: 1 x 4 = 4
- Add the numerator: 4 + 1 = 5
- Keep the same denominator: 4
Therefore, 1 ¼ is equivalent to the improper fraction ⁵/₄.
Finding Equivalent Fractions for ⁵/₄
Now that we have the improper fraction ⁵/₄, we can easily find equivalent fractions by multiplying both the numerator and denominator by the same number. Let's explore several examples:
- Multiply by 2: (5 x 2) / (4 x 2) = ¹⁰/₈
- Multiply by 3: (5 x 3) / (4 x 3) = ¹⁵/₁₂
- Multiply by 4: (5 x 4) / (4 x 4) = ²⁰/₁₆
- Multiply by 5: (5 x 5) / (4 x 5) = ²⁵/₂₀
- Multiply by 10: (5 x 10) / (4 x 10) = ⁵⁰/₄₀
All these fractions – ¹⁰/₈, ¹⁵/₁₂, ²⁰/₁₆, ²⁵/₂₀, ⁵⁰/₄₀ – are equivalent to ⁵/₄ and, consequently, to the original mixed number 1 ¼. They all represent the same value.
Simplifying Fractions: The Reverse Process
The reverse process of finding equivalent fractions involves simplifying fractions to their lowest terms. This means reducing the numerator and denominator to their smallest possible whole numbers while maintaining the same ratio. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD.
Let's take the example of ²⁰/₁₆:
- Find the GCD of 20 and 16: The GCD of 20 and 16 is 4.
- Divide both the numerator and denominator by the GCD: ²⁰/₄ = 5 and ¹⁶/₄ = 4
Therefore, ²⁰/₁₆ simplifies to ⁵/₄, confirming that it is equivalent to 1 ¼.
Visual Representation of Equivalent Fractions
Visual aids can greatly enhance the understanding of equivalent fractions. Imagine a rectangle divided into four equal parts. Shading five of these parts (one whole rectangle and one-quarter) visually represents ⁵/₄. Now, imagine dividing the same rectangle into eight equal parts. Shading ten of these parts would represent the equivalent fraction ¹⁰/₈. The area covered remains the same, illustrating that these fractions are equivalent. You can apply this visual method to other equivalent fractions we've discussed.
Practical Applications of Equivalent Fractions
Understanding equivalent fractions is vital in various mathematical applications:
- Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. Finding equivalent fractions allows you to convert fractions into a form that shares a common denominator.
- Comparing Fractions: Determining which fraction is larger or smaller is often easier when the fractions have a common denominator. Finding equivalent fractions facilitates this comparison.
- Solving Equations: Many algebraic equations involve fractions. Knowing how to manipulate and simplify fractions using equivalent fractions is essential for solving these equations.
- Real-world Problems: Many real-world problems involve fractional parts, such as measuring ingredients in cooking, calculating distances, or sharing resources. Understanding equivalent fractions helps in solving these problems accurately.
Beyond the Basics: Exploring More Complex Examples
Let's explore finding equivalent fractions for ⁵/₄ using slightly more complex approaches:
Using Decimals:
The fraction ⁵/₄ can be converted to a decimal by performing the division: 5 ÷ 4 = 1.25. Any decimal that equals 1.25 will represent an equivalent fraction. For example, 2.5/2, 3.75/3, 5/4, etc., will all have the same decimal equivalent. While not directly a fraction, this decimal representation can serve as a check when finding equivalent fractions.
Using Ratios:
Fractions can be understood as ratios. The ratio 5:4 is equivalent to 10:8, 15:12, and so on, reflecting the same proportional relationship. This ratio concept strengthens the understanding of equivalent fractions and their consistent relationship between numerator and denominator.
Common Mistakes to Avoid
When working with equivalent fractions, some common mistakes should be avoided:
- Only multiplying or dividing the numerator: Remember, you must always multiply or divide both the numerator and denominator by the same non-zero number to maintain the equivalent value.
- Incorrectly finding the GCD: An inaccurate greatest common divisor will lead to an incorrectly simplified fraction. Double-check your GCD calculation.
- Confusing equivalent fractions with simplification: Simplifying a fraction is a specific type of finding an equivalent fraction – the one with the smallest possible whole numbers in the numerator and denominator.
Conclusion: Mastering Equivalent Fractions
Understanding and finding equivalent fractions is a fundamental skill in mathematics with widespread applications. Mastering this concept strengthens your ability to work with fractions, solve problems effectively, and tackle more advanced mathematical concepts. By understanding the underlying principles and practicing the methods described in this article, you can confidently work with equivalent fractions and expand your mathematical knowledge. Remember the core concept: maintain the same ratio between the numerator and denominator when creating equivalent fractions. The diverse methods presented here – from basic multiplication to decimal conversions – provide a comprehensive understanding of this essential mathematical skill. Continue practicing, and you'll quickly master this crucial aspect of fractional arithmetic.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.