Which Fraction Is Equivalent To 6/8
News Co
Apr 27, 2025 · 5 min read
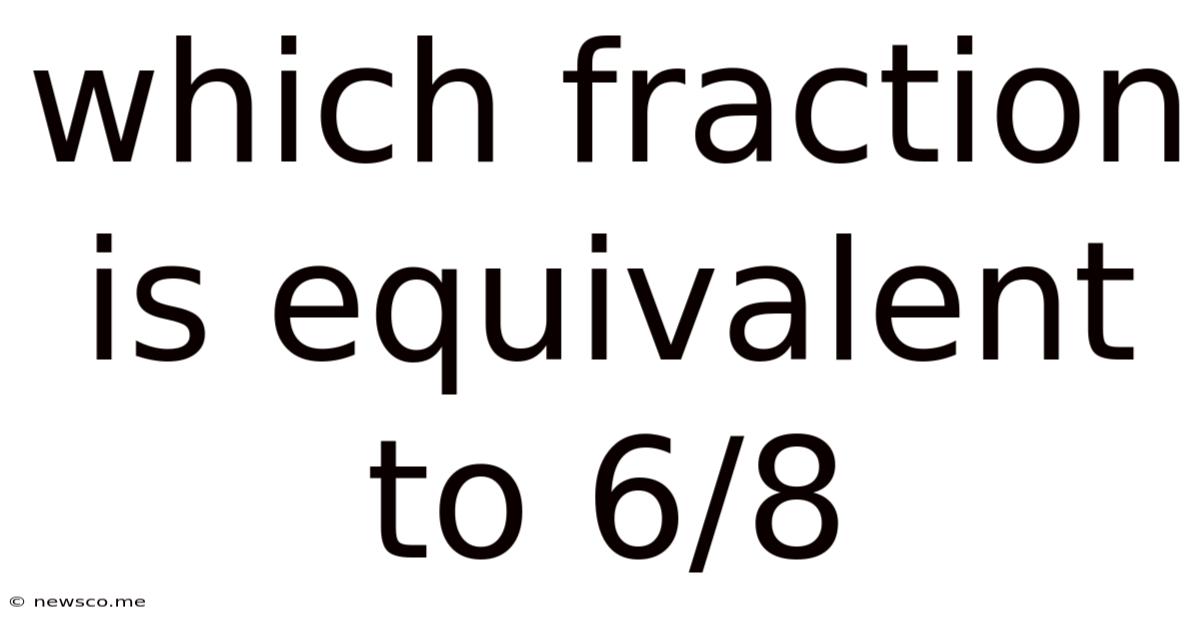
Table of Contents
Which Fraction is Equivalent to 6/8? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially for younger learners. However, understanding the underlying concepts of equivalent fractions is crucial for mastering more advanced mathematical concepts, from ratios and proportions to algebra and beyond. This comprehensive guide delves into the question, "Which fraction is equivalent to 6/8?", exploring the various methods for finding equivalent fractions and solidifying your understanding of this fundamental mathematical principle.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion of a whole, even though they are written differently. Think of it like this: cutting a pizza into 8 slices and taking 6 of them is exactly the same as cutting a smaller pizza into 4 slices and taking 3 of them. Both represent ¾ of the pizza. The key is that the ratio between the numerator (the top number) and the denominator (the bottom number) remains constant.
Key Concept: Equivalent fractions have the same value, even though they appear different. This is because you can multiply or divide both the numerator and the denominator by the same non-zero number without changing the overall value of the fraction.
Methods for Finding Equivalent Fractions
There are several effective methods to determine which fraction is equivalent to 6/8:
1. Simplifying Fractions (Finding the Simplest Form)
Simplifying a fraction means reducing it to its simplest form, where the numerator and the denominator have no common factors other than 1. This is also known as reducing or expressing the fraction in lowest terms.
To simplify 6/8, we need to find the greatest common divisor (GCD) of 6 and 8. The GCD is the largest number that divides both 6 and 8 without leaving a remainder. In this case, the GCD of 6 and 8 is 2.
Now, we divide both the numerator and the denominator by the GCD:
6 ÷ 2 = 3 8 ÷ 2 = 4
Therefore, the simplest form of 6/8 is 3/4. This means 6/8 and 3/4 are equivalent fractions.
2. Multiplying the Numerator and Denominator by the Same Number
We can create equivalent fractions by multiplying both the numerator and the denominator by the same number. This is based on the principle that multiplying a number by 1 doesn't change its value, and any number divided by itself equals 1.
For example, let's multiply both the numerator and the denominator of 3/4 by 2:
(3 x 2) / (4 x 2) = 6/8
This demonstrates that 3/4 and 6/8 are equivalent. We can use this method to generate infinitely many equivalent fractions. Multiplying by 3 gives us 9/12, multiplying by 4 gives 12/16, and so on. All these fractions are equivalent to 6/8 and 3/4.
3. Dividing the Numerator and Denominator by the Same Number
Conversely, we can find equivalent fractions by dividing both the numerator and denominator by the same number, provided that both numbers are divisible by that number without leaving a remainder. This method is essentially the reverse of the previous method and leads to simplifying the fraction.
As shown earlier, dividing 6/8 by the GCD (2) gives us the simplest form, 3/4.
Visual Representation of Equivalent Fractions
Visual aids are extremely helpful, particularly for younger learners, in understanding the concept of equivalent fractions. Imagine a rectangular shape representing a whole.
- 6/8: Divide the rectangle into 8 equal parts and shade 6 of them.
- 3/4: Divide the same-sized rectangle into 4 equal parts and shade 3 of them.
You'll visually see that both representations cover the same area, demonstrating that 6/8 and 3/4 are equivalent. You can use this visual method with other equivalent fractions derived by multiplying the numerator and denominator of 3/4 by the same number.
Applications of Equivalent Fractions in Real-World Scenarios
The concept of equivalent fractions is not just a theoretical exercise; it has practical applications in numerous real-world situations:
- Cooking and Baking: Recipes often require adjusting ingredient amounts. If a recipe calls for 1/2 cup of sugar and you want to double the recipe, you'll need 1 cup (which is equivalent to 2/2 cups).
- Measurement: Converting between different units of measurement frequently involves equivalent fractions. For example, converting inches to feet or centimeters to meters utilizes this concept.
- Sharing and Division: Dividing items fairly among a group often requires understanding equivalent fractions.
- Probability: Calculating probabilities frequently involves working with equivalent fractions to simplify and interpret results.
- Geometry: Finding the area or volume of shapes often involves using fractions and requires simplifying and working with equivalent fractions.
Beyond 6/8: Practicing with Other Fractions
Once you understand the principles behind finding equivalent fractions for 6/8, you can apply the same techniques to any other fraction. The key steps are:
- Find the greatest common divisor (GCD) of the numerator and the denominator. This allows you to simplify the fraction to its lowest terms.
- Multiply both the numerator and denominator by the same number to create larger equivalent fractions.
- Divide both the numerator and denominator by the same number (a common factor) to find simpler equivalent fractions. Remember you must be able to divide both numbers evenly.
Practicing with different fractions helps reinforce the concept and build confidence in your ability to work with fractions effectively.
Common Mistakes to Avoid
While finding equivalent fractions is generally straightforward, certain common mistakes should be avoided:
- Only multiplying or dividing the numerator or denominator: Remember, to maintain equivalence, you must perform the same operation (multiplication or division) on both the numerator and the denominator.
- Using different numbers for the numerator and denominator: The numbers you multiply or divide by must be identical for both the numerator and denominator.
- Forgetting to simplify to lowest terms: Simplifying to the lowest terms ensures a clearer and more concise representation of the fraction.
Conclusion: Mastering Equivalent Fractions
Understanding equivalent fractions is a cornerstone of mathematical proficiency. This guide has explored various methods for determining which fraction is equivalent to 6/8 and provided a framework for tackling similar problems. By mastering the techniques outlined above and practicing regularly, you'll build a strong foundation for more advanced mathematical concepts and effectively apply this knowledge to diverse real-world situations. Remember, the key is to understand the fundamental principle that equivalent fractions represent the same portion of a whole, regardless of their appearance. Practice makes perfect, so keep practicing and soon you'll be a fraction master!
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 6/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.