Which Is A Factor Of X2+8x-48
News Co
Mar 22, 2025 · 5 min read
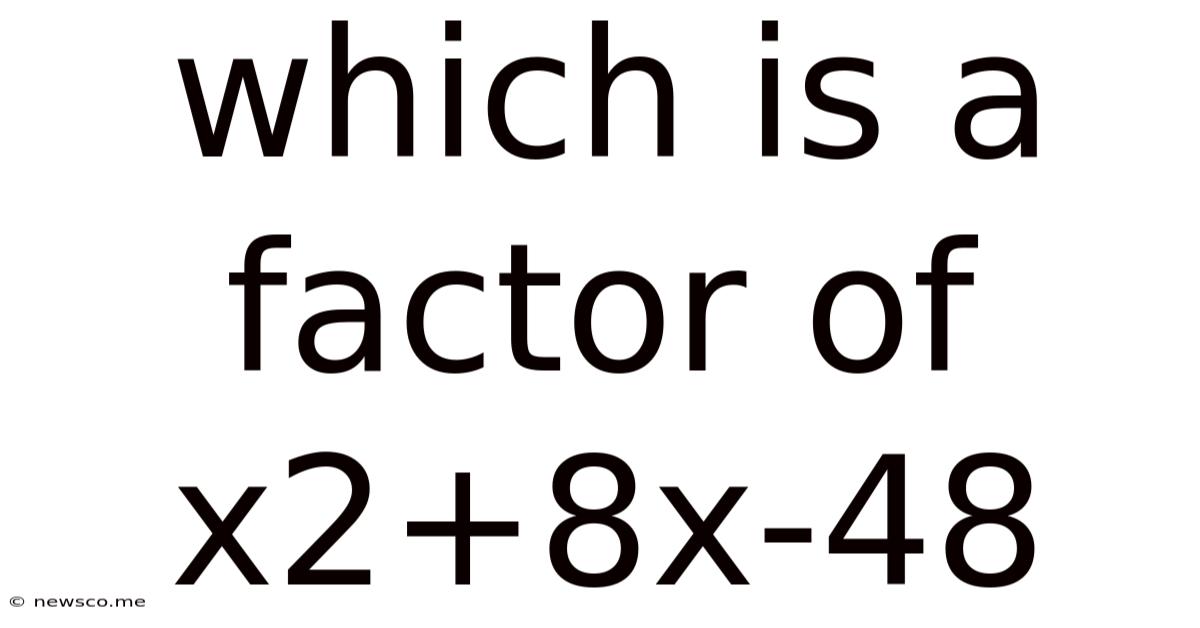
Table of Contents
Which is a Factor of x² + 8x - 48? A Comprehensive Guide to Factoring Quadratic Expressions
Finding the factors of a quadratic expression like x² + 8x - 48 is a fundamental skill in algebra. This seemingly simple problem opens the door to understanding more complex mathematical concepts. This comprehensive guide will not only answer the question of which expression is a factor but also provide you with a thorough understanding of the process, equipping you to tackle similar problems with confidence.
Understanding Quadratic Expressions
Before diving into the factorization, let's establish a solid foundation. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants. In our case, a = 1, b = 8, and c = -48.
Key Terms: Factors and Factoring
- Factors: Factors are numbers or expressions that divide evenly into a given number or expression without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
- Factoring: Factoring is the process of breaking down a number or expression into its factors. It's like reverse multiplication.
Methods for Factoring Quadratic Expressions
There are several methods to factor quadratic expressions. We'll explore the most common and effective techniques, focusing on the one most suitable for x² + 8x - 48.
1. The AC Method (for Quadratics with a leading coefficient of 1)
Since our quadratic expression, x² + 8x - 48, has a leading coefficient (a) of 1, the AC method simplifies significantly. This method involves finding two numbers that add up to 'b' (the coefficient of x) and multiply to 'ac' (the product of the coefficient of x² and the constant term).
Steps:
- Identify 'b' and 'ac': In our expression, b = 8 and ac = (1)(-48) = -48.
- Find two numbers: We need two numbers that add up to 8 and multiply to -48. Let's brainstorm:
- 12 and -4 satisfy these conditions (12 + (-4) = 8 and 12 * (-4) = -48).
- Rewrite the expression: Rewrite the middle term (8x) using the two numbers we found: x² + 12x - 4x - 48.
- Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- x(x + 12) - 4(x + 12)
- Factor out the common binomial: Notice that (x + 12) is common to both terms. Factor it out:
- (x + 12)(x - 4)
Therefore, the factors of x² + 8x - 48 are (x + 12) and (x - 4).
2. The Trial and Error Method (for Quadratics with a leading coefficient of 1)
This method is a quicker approach, particularly useful when the quadratic has a leading coefficient of 1. It relies on intuition and testing different combinations of factors.
Steps:
- Set up the binomial factors: Since the leading coefficient is 1, we know the factors will be of the form (x + p)(x + q), where 'p' and 'q' are numbers that add up to 'b' (8) and multiply to 'c' (-48).
- Find the correct factors: Through trial and error, we find that 12 and -4 are the numbers that work.
- Write the factored form: (x + 12)(x - 4)
This method again confirms that (x + 12) and (x - 4) are the factors of x² + 8x - 48.
3. Using the Quadratic Formula (A More General Approach)
While not directly a factoring method, the quadratic formula can help find the roots (or zeros) of the quadratic equation. These roots are directly related to the factors.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
For x² + 8x - 48, a = 1, b = 8, and c = -48. Substituting these values:
x = [-8 ± √(8² - 4 * 1 * -48)] / 2 * 1 x = [-8 ± √(64 + 192)] / 2 x = [-8 ± √256] / 2 x = [-8 ± 16] / 2
This gives us two solutions:
x = (-8 + 16) / 2 = 4 x = (-8 - 16) / 2 = -12
The roots are 4 and -12. Since the roots are the values that make the expression equal to zero, we can write the factors as (x - 4) and (x + 12).
This confirms, once again, that (x + 12) and (x - 4) are the factors of x² + 8x - 48.
Verifying the Factors
It's always a good practice to verify the factors by expanding them. Let's expand (x + 12)(x - 4):
(x + 12)(x - 4) = x² - 4x + 12x - 48 = x² + 8x - 48
This confirms our factorization is correct.
Applications of Factoring Quadratic Expressions
Factoring quadratic expressions is not just an academic exercise; it has significant applications in various fields, including:
- Solving Quadratic Equations: Factoring allows us to solve quadratic equations easily by setting each factor to zero. This is crucial in numerous real-world problems involving projectiles, areas, and optimization.
- Calculus: Factoring is a fundamental step in simplifying expressions and solving problems in calculus, especially when dealing with derivatives and integrals.
- Physics and Engineering: Many physical phenomena can be modeled using quadratic equations, and factoring helps in analyzing and solving these models.
- Computer Science: Factoring is used in algorithm design and cryptography.
Beyond x² + 8x - 48: Tackling More Complex Quadratics
While we've focused on x² + 8x - 48, the methods discussed can be applied to a wider range of quadratic expressions, even those with leading coefficients other than 1. For quadratics with a leading coefficient not equal to 1, the AC method becomes more involved, but the fundamental principle remains the same.
Remember to always:
- Look for common factors: Before applying any method, check if the terms in the expression share any common factors. Factoring out the common factor simplifies the expression.
- Practice regularly: The more you practice factoring, the faster and more proficient you'll become.
- Use different methods: Try different approaches; some methods might be better suited for certain types of quadratics than others.
This comprehensive guide has not only answered the question of which expression is a factor of x² + 8x - 48 but also provided you with a deep understanding of the process of factoring quadratic expressions and its practical applications. By mastering these techniques, you’ll be well-equipped to tackle more complex algebraic problems and unlock a deeper understanding of mathematics. Remember to practice regularly and explore different methods to solidify your understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Is A Factor Of X2+8x-48 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.