Which Is A Factor Of X2-9x+14
News Co
Mar 22, 2025 · 5 min read
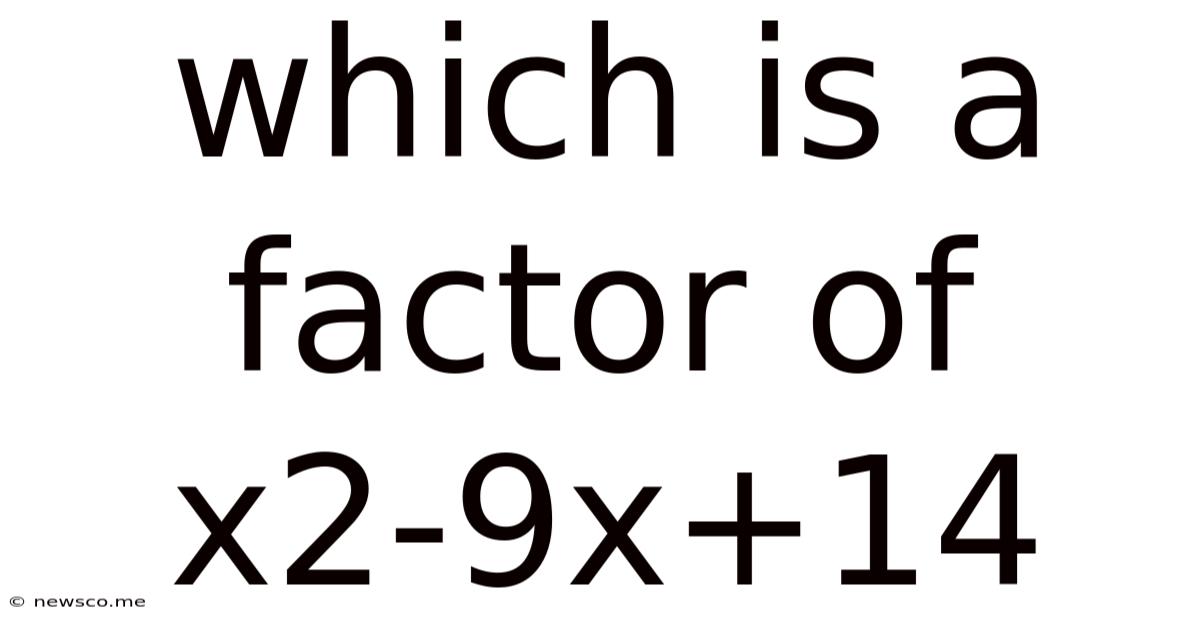
Table of Contents
Which is a Factor of x² - 9x + 14? A Comprehensive Guide to Factoring Quadratic Equations
Factoring quadratic equations is a fundamental skill in algebra. Understanding how to factor these equations efficiently and accurately is crucial for solving a wide range of mathematical problems. This article delves deep into factoring the quadratic expression x² - 9x + 14, explaining the process step-by-step, exploring different methods, and providing additional examples to solidify your understanding. We'll also touch upon the broader context of quadratic equations and their applications.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (typically 'x') is 2. The general form of a quadratic equation is:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Factoring a quadratic expression (like x² - 9x + 14) involves finding two expressions that, when multiplied together, give the original expression. This is crucial for solving the quadratic equation when set to zero.
Factoring x² - 9x + 14: The Step-by-Step Approach
Let's break down the process of factoring x² - 9x + 14. We're looking for two binomials (expressions with two terms) that multiply to give our quadratic. The most common method is using the following steps:
-
Identify the coefficients: In our equation, a = 1, b = -9, and c = 14.
-
Find two numbers that add up to 'b' and multiply to 'c': We need two numbers that add up to -9 and multiply to 14. Let's consider the factors of 14: 1 and 14, 2 and 7. Since the sum needs to be -9, and the product is positive, both numbers must be negative. Therefore, -2 and -7 satisfy both conditions (-2 + -7 = -9 and -2 * -7 = 14).
-
Write the factors: Using the numbers we found, we can write the factored form of the quadratic expression as:
(x - 2)(x - 7)
- Verify the factorization: To check our work, we can expand the factored form using the FOIL method (First, Outer, Inner, Last):
- First: x * x = x²
- Outer: x * -7 = -7x
- Inner: -2 * x = -2x
- Last: -2 * -7 = 14
Combining these terms gives us x² - 7x - 2x + 14 = x² - 9x + 14. This matches our original expression, confirming our factorization is correct.
Therefore, (x - 2) and (x - 7) are the factors of x² - 9x + 14.
Alternative Methods for Factoring Quadratic Expressions
While the method above is widely used, other techniques can be employed to factor quadratic expressions, especially when dealing with more complex equations. These include:
-
The AC Method: This method is particularly useful when the coefficient 'a' is not equal to 1. It involves multiplying 'a' and 'c', finding two numbers that add up to 'b' and multiply to 'ac', and then rewriting the quadratic expression before factoring.
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, which can then be easily factored.
-
Quadratic Formula: This formula provides the roots (solutions) of a quadratic equation, which can be used to determine the factors. The quadratic formula is:
x = (-b ± √(b² - 4ac)) / 2a
While these methods are valuable, for simple quadratics like x² - 9x + 14, the direct method explained earlier is the most efficient.
Applications of Factoring Quadratic Equations
Factoring quadratic equations is not just a theoretical exercise; it has numerous practical applications across various fields, including:
-
Physics: Solving projectile motion problems, analyzing the trajectory of objects under the influence of gravity.
-
Engineering: Designing structures, calculating forces and stresses in materials.
-
Economics: Modeling supply and demand curves, optimizing production levels.
-
Computer Science: Developing algorithms, solving optimization problems.
-
Finance: Calculating compound interest, determining investment returns.
The ability to factor quadratic equations is fundamental to tackling these real-world problems effectively.
Solving Quadratic Equations Using Factors
Once you've factored a quadratic expression, you can use the factors to solve the corresponding quadratic equation. For example, to solve x² - 9x + 14 = 0, we use the factored form (x - 2)(x - 7) = 0. This equation is true if either (x - 2) = 0 or (x - 7) = 0. Therefore, the solutions (roots) of the equation are x = 2 and x = 7.
Advanced Factoring Techniques and Challenges
While x² - 9x + 14 is a relatively straightforward example, more complex quadratic expressions may require more advanced techniques. For instance:
-
Quadratics with a leading coefficient other than 1: These require methods like the AC method or grouping.
-
Quadratics that are not factorable using integers: Some quadratic expressions cannot be factored using integers. In these cases, the quadratic formula or completing the square are necessary to find the roots.
-
Higher-degree polynomials: Similar factoring principles extend to higher-degree polynomials, although the methods become more intricate.
Practice Problems
To solidify your understanding, try factoring the following quadratic expressions:
- x² + 5x + 6
- x² - 4x - 12
- 2x² + 7x + 3
- 3x² - 10x + 8
Conclusion: Mastering Quadratic Factoring
Mastering the skill of factoring quadratic equations is a cornerstone of algebraic proficiency. This article provided a detailed guide to factoring x² - 9x + 14, demonstrating various methods and exploring the broader applications of this crucial mathematical concept. By understanding the underlying principles and practicing regularly, you can build a strong foundation in algebra and successfully tackle more complex mathematical problems. Remember, consistent practice is key to developing fluency in factoring and solving quadratic equations. Keep practicing, and you'll find this process becomes increasingly intuitive and efficient.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Which Is A Factor Of X2-9x+14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.