Which Is A Solution To X 2 X 10 13
News Co
Mar 21, 2025 · 4 min read
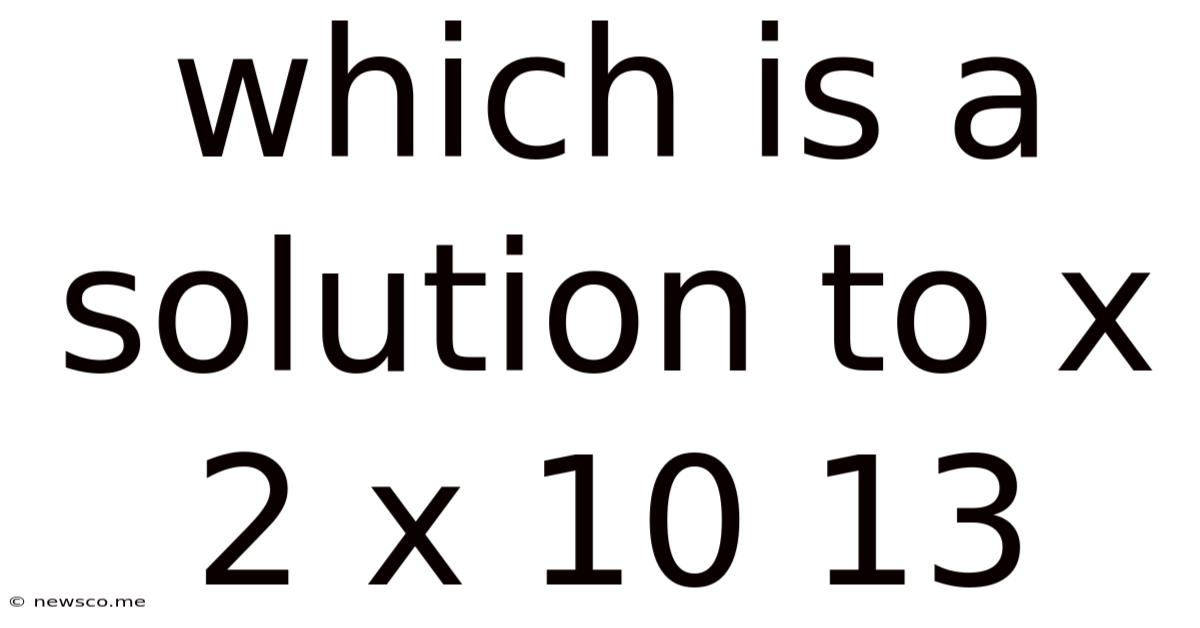
Table of Contents
Decoding the Solution: x² = 10¹³
The equation x² = 10¹³ presents a seemingly simple mathematical challenge: find the value of x. However, a deeper dive reveals nuances that extend beyond a simple square root calculation. This exploration delves into the various methods of solving this equation, analyzing the nature of the solution, and considering the practical implications and interpretations within different mathematical contexts.
Understanding the Problem: x² = 10¹³
At its core, the equation x² = 10¹³ is a quadratic equation where the coefficient of x is zero. The number 10¹³ represents a tremendously large number (ten trillion), highlighting the scale of the solution we seek. A straightforward approach would involve taking the square root of both sides:
x = ±√10¹³
This immediately introduces a key point: the equation has two solutions, one positive and one negative. While seemingly trivial, this duality is crucial for understanding the complete solution set and its implications within various applications.
Method 1: Direct Calculation using a Calculator or Software
The most straightforward method is to use a calculator or mathematical software to directly compute the square root of 10¹³. Most scientific calculators and programming languages (like Python, MATLAB, etc.) can handle such calculations with ease. The result will be an approximation, as the square root of 10¹³ is an irrational number.
The approximate solutions would be:
x ≈ ±3,162,277.66
This simple approach offers a quick numerical answer, suitable for many practical situations where high precision isn't paramount. However, it doesn't provide insight into the underlying mathematical properties or the potential for more refined solutions.
Method 2: Logarithmic Approach for Enhanced Precision
For enhanced precision and a deeper understanding, a logarithmic approach can be employed. Recall the logarithmic property: log(aᵇ) = b * log(a). Applying this to our equation:
log(x²) = log(10¹³)
2 * log(x) = 13 * log(10)
Since log₁₀(10) = 1, we simplify to:
2 * log(x) = 13
log(x) = 6.5
Now, we need to find the antilog (inverse logarithm) of 6.5. This can be done using a calculator or software, or by using the definition of logarithms:
x = 10⁶·⁵
This expression is equivalent to √10¹³, offering a more precise way to calculate the solution using logarithmic properties. This method allows for precise calculations even with larger exponents.
Method 3: Iterative Methods for Approximations
For situations where computational resources are limited or for educational purposes, iterative methods like the Babylonian method (also known as Heron's method) can be used to approximate the square root. This method involves repeatedly refining an initial guess until the desired level of accuracy is achieved.
The Babylonian method formula is:
xₙ₊₁ = (xₙ + a/xₙ) / 2
where:
- xₙ is the current approximation
- xₙ₊₁ is the next approximation
- a is the number whose square root is being sought (in our case, 10¹³)
Starting with an initial guess (e.g., x₀ = 10⁶), the formula is iteratively applied until the difference between successive approximations is smaller than a predefined tolerance. This method demonstrates the iterative process of approximating solutions, which is crucial in various numerical analysis techniques.
Implications and Interpretations in Different Contexts
The solutions x ≈ ±3,162,277.66 have varied interpretations depending on the context of the problem.
-
Physics: In physics, this equation might represent a relationship between two physical quantities. The positive and negative solutions could represent different directions or phases.
-
Engineering: In engineering design, the solution might represent a dimension or a parameter, where the positive solution is typically relevant, and the negative one is discarded as physically unfeasible.
-
Computer Science: In computer science, such calculations can appear in algorithms related to scaling, data structures, or performance analysis. The magnitude of the solution highlights the computational complexity involved.
-
Mathematics: Purely mathematically, both solutions are equally valid, showcasing the properties of quadratic equations and the importance of considering all possible solutions.
Expanding the Scope: Variations and Extensions
The core equation x² = 10¹³ can be extended to more complex scenarios:
-
Adding a Constant: x² + c = 10¹³, where 'c' is a constant. This transforms the equation into a slightly more complex quadratic equation that requires the quadratic formula for solution.
-
Introducing a Linear Term: ax² + bx + c = 10¹³, where 'a', 'b', and 'c' are constants. This introduces a more general quadratic equation solvable using the quadratic formula. The solutions will depend heavily on the values of the coefficients.
-
Higher-Order Equations: The concept extends to higher-order polynomial equations where the power of 'x' is greater than 2. These equations require more advanced techniques like numerical methods or factoring for solutions.
Conclusion: Beyond a Simple Calculation
Solving x² = 10¹³ transcends a simple square root calculation. It underscores the importance of understanding the nature of the solutions, the different methods available for solving the equation, and the diverse interpretations within various fields. Whether using a direct calculation, logarithmic approach, or iterative methods, understanding the underlying mathematical principles enhances problem-solving skills and illuminates the power and versatility of mathematical tools. The magnitude of the solution also highlights the scale and complexity that can arise in seemingly simple mathematical expressions, prompting further investigation and exploration into more intricate mathematical concepts. By analyzing this seemingly straightforward equation, we gain valuable insights into the depth and breadth of mathematical problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Is A Solution To X 2 X 10 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.