Which Is Bigger 0.25 Or 0.5
News Co
Apr 27, 2025 · 4 min read
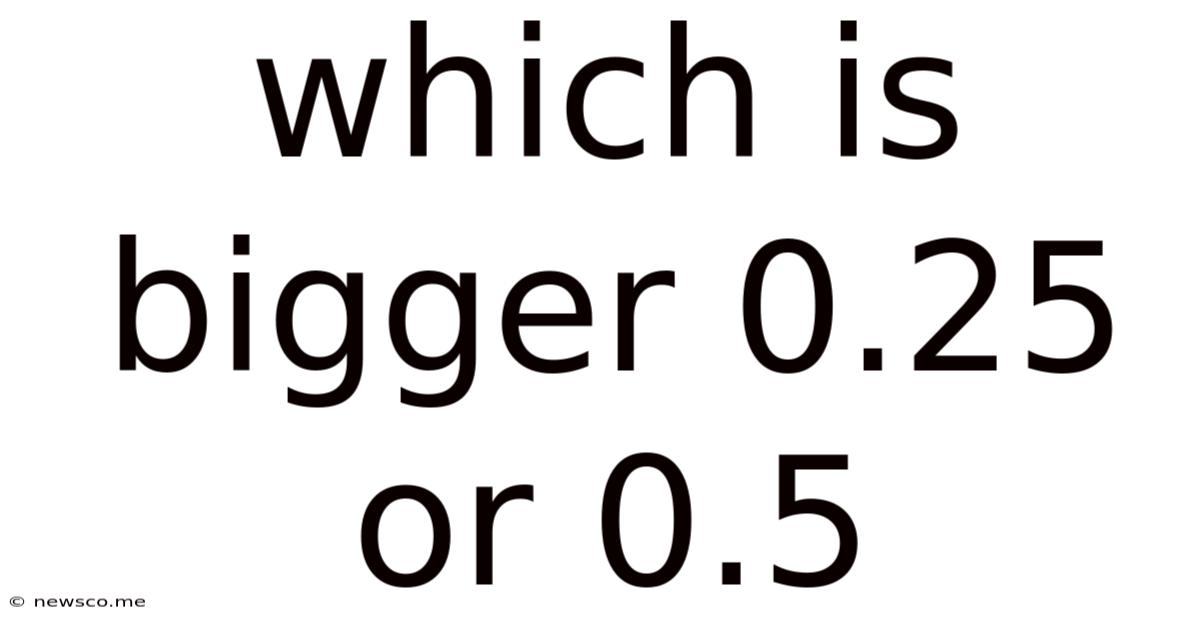
Table of Contents
Which is Bigger: 0.25 or 0.5? A Deep Dive into Decimal Comparison
Understanding decimal numbers is fundamental to mathematics and numerous real-world applications. This seemingly simple question – which is bigger, 0.25 or 0.5? – provides a perfect springboard to explore the concepts of decimal representation, place value, and various methods for comparing decimal numbers. While the answer itself is straightforward, the journey of understanding why one is larger than the other is crucial for building a strong mathematical foundation.
Understanding Decimal Representation
Before we delve into the comparison, let's solidify our understanding of decimals. Decimal numbers are a way of representing numbers that are not whole numbers. They utilize a base-ten system, where each digit to the right of the decimal point represents a fraction of a power of ten.
- 0.1: Represents one-tenth (1/10)
- 0.01: Represents one-hundredth (1/100)
- 0.001: Represents one-thousandth (1/1000) and so on.
Each position to the right of the decimal point holds a decreasing value. This is crucial when comparing decimal numbers.
Comparing 0.25 and 0.5: A Visual Approach
One of the easiest ways to understand the difference between 0.25 and 0.5 is to visualize them. Imagine a whole unit, like a pizza, divided into parts.
-
0.5: This represents one-half (1/2) of the pizza. If you cut the pizza in half, 0.5 represents one of those halves.
-
0.25: This represents one-quarter (1/4) of the pizza. If you cut the pizza into four equal slices, 0.25 represents one of those slices.
Clearly, half of a pizza is larger than one-quarter of a pizza. This visual representation makes it immediately apparent that 0.5 is bigger than 0.25.
Comparing 0.25 and 0.5: A Numerical Approach
While the visual approach is intuitive, a numerical approach strengthens our understanding and allows us to compare more complex decimals.
We can convert both decimals into fractions to compare them directly:
- 0.5 = 5/10 = 1/2 (Simplifying the fraction)
- 0.25 = 25/100 = 1/4 (Simplifying the fraction)
Now we have a straightforward comparison: 1/2 versus 1/4. Since halves are larger than quarters, we confirm that 0.5 is bigger than 0.25.
We can also express both decimals as fractions with a common denominator:
- 0.5 = 50/100
- 0.25 = 25/100
Again, it's clear that 50/100 is larger than 25/100, solidifying the fact that 0.5 > 0.25.
The Importance of Place Value in Decimal Comparison
The concept of place value is paramount in comparing decimals. Let's analyze the place value of each digit in 0.25 and 0.5:
0.5: The digit 5 is in the tenths place, representing 5/10 or 0.5.
0.25: The digit 2 is in the tenths place, representing 2/10 or 0.2. The digit 5 is in the hundredths place, representing 5/100 or 0.05. Therefore, 0.25 = 0.2 + 0.05.
By comparing the tenths place, we see that 0.5 (five tenths) is greater than 0.2 (two tenths). This difference alone is enough to determine that 0.5 is bigger.
Advanced Decimal Comparison Techniques
While the comparison between 0.25 and 0.5 is straightforward, more complex decimal comparisons require a systematic approach. Here are some useful techniques:
-
Comparing Digit by Digit: Start by comparing the digits in the tenths place. If they are different, the decimal with the larger digit in the tenths place is bigger. If they are the same, move to the hundredths place, and so on.
-
Adding Zeros to Equalize Decimal Places: When comparing decimals with different numbers of decimal places, add trailing zeros to the shorter decimal to make the comparison easier. For example, comparing 0.5 and 0.25 can be rewritten as 0.50 and 0.25.
-
Converting to Fractions: Converting decimals to fractions can often simplify the comparison, particularly when dealing with recurring decimals or fractions.
-
Using a Number Line: A number line provides a visual representation of the relative size of decimal numbers. Plotting 0.25 and 0.5 on a number line clearly demonstrates that 0.5 lies to the right of 0.25, indicating that it is larger.
Real-World Applications of Decimal Comparison
Understanding decimal comparison is crucial in various real-world scenarios:
-
Finance: Comparing prices, interest rates, discounts, and stock values all involve comparing decimal numbers.
-
Measurement: Many measurements, such as length, weight, and volume, utilize decimal numbers. Accurate comparisons are essential for tasks like construction, engineering, and scientific research.
-
Science: Scientific data often involves decimal numbers, and comparing these values is critical for analysis and interpretation.
-
Technology: Computer programming, data analysis, and many other technological fields heavily rely on decimal number manipulation and comparison.
Conclusion: Mastering Decimal Comparison
The question of which is bigger, 0.25 or 0.5, serves as a gateway to understanding the intricacies of decimal numbers. Through visual representation, numerical analysis, and the understanding of place value, we’ve clearly established that 0.5 is greater than 0.25. Mastering decimal comparison techniques is crucial for success in various academic and professional fields. By solidifying your understanding of decimal representation and applying the appropriate comparison methods, you can confidently tackle even the most complex decimal comparisons. Remember to practice regularly to build your proficiency and confidence in this fundamental mathematical skill. The more you practice, the easier and more intuitive decimal comparisons will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Is Bigger 0.25 Or 0.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.