Which Is Bigger 1 3 Or 3 8
News Co
Apr 24, 2025 · 5 min read
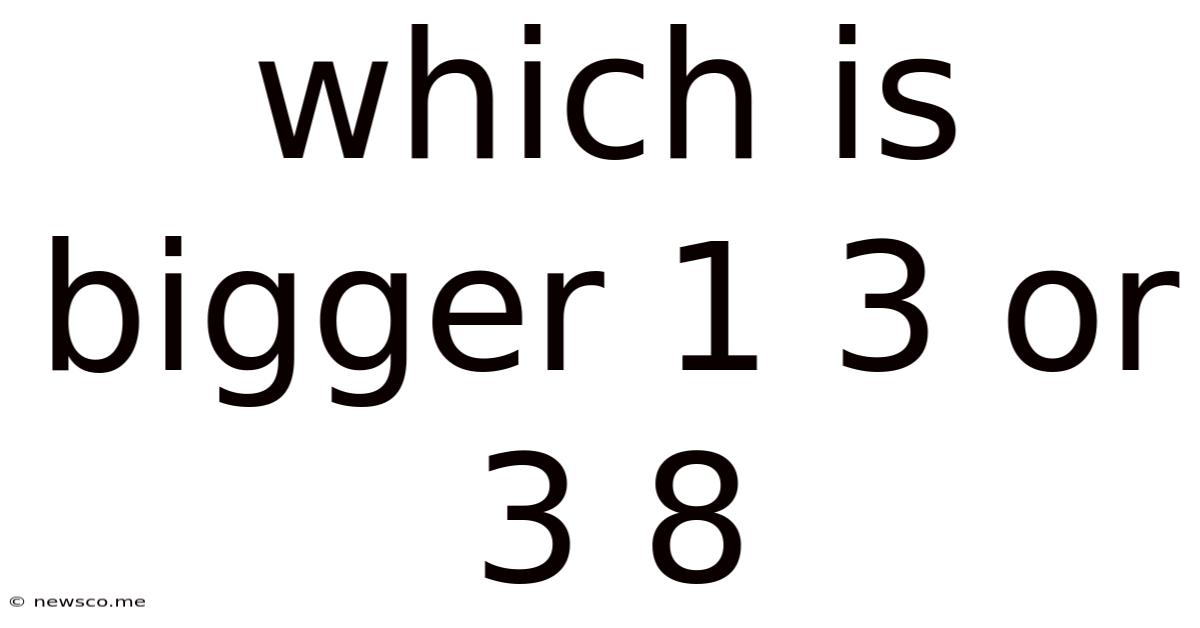
Table of Contents
Which is Bigger: 1/3 or 3/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, essential for various applications from everyday life to complex scientific calculations. This article will comprehensively explore the comparison of two common fractions: 1/3 and 3/8. We'll delve into multiple methods for determining which is larger, explaining the underlying principles clearly and providing practical examples to solidify your understanding. By the end, you'll not only know which fraction is bigger but also possess a robust understanding of fraction comparison techniques.
Understanding Fractions: A Quick Refresher
Before jumping into the comparison, let's briefly revisit the fundamental components of a fraction:
- Numerator: The top number in a fraction, representing the number of parts you have.
- Denominator: The bottom number in a fraction, representing the total number of equal parts the whole is divided into.
For example, in the fraction 1/3, 1 is the numerator and 3 is the denominator. This signifies that we have 1 part out of a total of 3 equal parts. Similarly, in 3/8, 3 is the numerator and 8 is the denominator, meaning we have 3 parts out of a total of 8 equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. Once this is achieved, we can directly compare the numerators.
Steps:
-
Find the Least Common Multiple (LCM): The LCM of the denominators (3 and 8) is the smallest number that both 3 and 8 divide into evenly. The LCM of 3 and 8 is 24.
-
Convert the Fractions: To convert 1/3 to have a denominator of 24, we multiply both the numerator and the denominator by 8 (24/3 = 8):
(1 * 8) / (3 * 8) = 8/24
To convert 3/8 to have a denominator of 24, we multiply both the numerator and the denominator by 3 (24/8 = 3):
(3 * 3) / (8 * 3) = 9/24
-
Compare the Numerators: Now that both fractions have the same denominator (24), we can directly compare their numerators: 8 and 9. Since 9 > 8, we can conclude that 9/24 > 8/24.
Conclusion: Therefore, 3/8 (which is equal to 9/24) is bigger than 1/3 (which is equal to 8/24).
Method 2: Converting to Decimals
Another effective way to compare fractions is by converting them to their decimal equivalents. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator.
Steps:
-
Divide the Numerator by the Denominator: To convert 1/3 to a decimal, divide 1 by 3:
1 ÷ 3 ≈ 0.333... (a repeating decimal)
-
Divide the Numerator by the Denominator: To convert 3/8 to a decimal, divide 3 by 8:
3 ÷ 8 = 0.375
-
Compare the Decimals: Now compare the decimal values: 0.375 and 0.333... Since 0.375 > 0.333..., we conclude that 3/8 is bigger than 1/3.
Method 3: Visual Representation
A visual approach can be highly intuitive, especially for those new to fraction comparison. This method involves representing the fractions graphically.
Imagine two identical circles.
-
Representing 1/3: Divide the first circle into three equal parts. Shade one part to represent 1/3.
-
Representing 3/8: Divide the second circle into eight equal parts. Shade three parts to represent 3/8.
By visually comparing the shaded areas, it becomes evident that the shaded area representing 3/8 is larger than the shaded area representing 1/3. This confirms that 3/8 > 1/3. While not as precise as the other methods for more complex fractions, this approach helps build an intuitive understanding of fraction size.
Method 4: Cross-Multiplication
This is a shortcut method for comparing two fractions. It avoids the need to find a common denominator directly.
Steps:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa.
1/3 and 3/8
1 * 8 = 8 3 * 3 = 9
-
Compare the Products: Compare the two products. The fraction corresponding to the larger product is the larger fraction. Since 9 > 8, 3/8 is larger than 1/3.
Practical Applications: Why This Matters
Understanding fraction comparison is crucial in many real-world situations:
-
Cooking and Baking: Following recipes often involves working with fractions of ingredients. Knowing which fraction is larger helps ensure accurate measurements.
-
Construction and Engineering: Precision in construction and engineering requires accurate calculations involving fractions of measurements.
-
Finance and Accounting: Working with budgets and financial statements involves manipulating fractions and percentages.
-
Data Analysis: Interpreting data often necessitates comparing fractions and percentages to draw meaningful conclusions.
-
Everyday Life: Sharing resources fairly, dividing tasks, or understanding discounts all involve understanding fractions.
Beyond the Basics: Extending Your Knowledge
While this article focuses on comparing 1/3 and 3/8, the methods discussed are applicable to any two fractions. To further enhance your understanding, consider exploring these related concepts:
-
Improper Fractions and Mixed Numbers: Learn how to convert between improper fractions (where the numerator is larger than or equal to the denominator) and mixed numbers (a combination of a whole number and a fraction).
-
Equivalent Fractions: Understand how to find equivalent fractions (fractions that represent the same value) by multiplying or dividing both the numerator and denominator by the same number.
-
Adding, Subtracting, Multiplying, and Dividing Fractions: Master these fundamental operations to work confidently with fractions in more complex scenarios.
Conclusion: Mastering Fraction Comparison
Comparing fractions effectively is a key mathematical skill. By understanding the methods outlined—finding a common denominator, converting to decimals, visual representation, and cross-multiplication—you can confidently determine which fraction is larger in any given situation. Remember that practice is key to mastering these techniques. The more you practice, the more intuitive fraction comparison will become, empowering you to tackle more complex mathematical problems and real-world scenarios with confidence. This thorough understanding will equip you with a valuable tool applicable across various fields and daily life.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1 3 Or 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.