Which Is F 5 For The Function 2x2 2x 3
News Co
Mar 14, 2025 · 5 min read
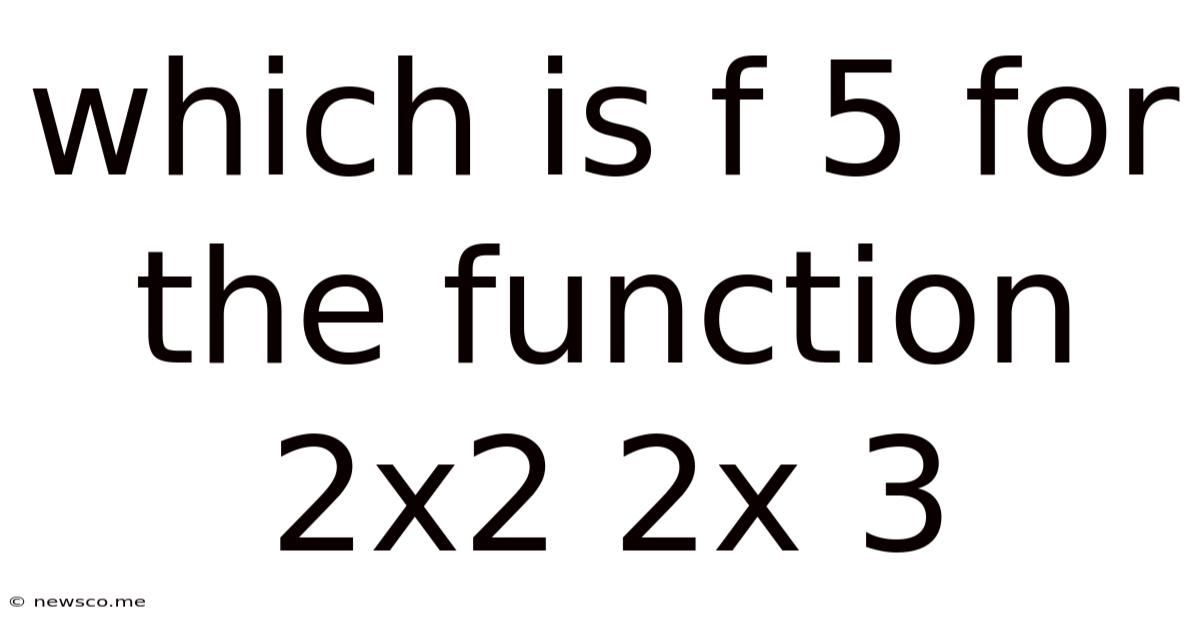
Table of Contents
Finding f(5) for the Function f(x) = 2x² + 2x + 3
Finding the value of a function at a specific point is a fundamental concept in algebra and calculus. This article will guide you through the process of determining f(5) for the quadratic function f(x) = 2x² + 2x + 3, explaining the steps involved and exploring related concepts. We'll also delve into broader applications of function evaluation and its importance in various fields.
Understanding the Function f(x) = 2x² + 2x + 3
Before we calculate f(5), let's understand the function itself. f(x) = 2x² + 2x + 3 is a quadratic function, meaning it's a polynomial of degree 2. Its graph is a parabola. The general form of a quadratic function is ax² + bx + c, where 'a', 'b', and 'c' are constants. In our case:
- a = 2: This determines the parabola's shape (opens upwards since a > 0).
- b = 2: This influences the parabola's position and slope.
- c = 3: This is the y-intercept (the point where the parabola crosses the y-axis).
Calculating f(5)
To find f(5), we simply substitute x = 5 into the function:
f(x) = 2x² + 2x + 3
f(5) = 2(5)² + 2(5) + 3
Following the order of operations (PEMDAS/BODMAS), we first handle the exponent:
f(5) = 2(25) + 2(5) + 3
Next, we perform the multiplications:
f(5) = 50 + 10 + 3
Finally, we add the terms:
f(5) = 63
Therefore, the value of the function f(x) = 2x² + 2x + 3 at x = 5 is 63.
Visualizing the Function and f(5)
Imagine the graph of the parabola representing f(x) = 2x² + 2x + 3. The point (5, 63) lies on this parabola. This point represents the output (63) of the function when the input is 5. Visualizing this helps solidify the understanding of function evaluation. While we won't create a graph here, consider using graphing calculators or software to plot the function and see the point (5, 63) clearly.
Applications of Function Evaluation
Function evaluation is not just an abstract mathematical exercise. It has wide-ranging applications across various fields:
1. Physics and Engineering:
- Projectile Motion: Functions describe the trajectory of projectiles. Evaluating the function at different time points gives the projectile's position.
- Electrical Circuits: Functions model current, voltage, and resistance. Evaluating these functions helps determine the circuit's behavior at specific times or under varying conditions.
- Mechanical Engineering: Functions are crucial in analyzing stress, strain, and other mechanical properties of materials.
2. Economics and Finance:
- Predictive Modeling: Economic models use functions to predict future trends based on current data. Evaluating these functions helps forecast economic indicators.
- Investment Analysis: Functions describe the growth of investments. Evaluating these functions helps determine the future value of investments.
- Risk Assessment: Financial models use functions to assess risk and potential losses.
3. Computer Science:
- Algorithms and Data Structures: Functions are fundamental to programming. Evaluating functions is essential for executing algorithms and manipulating data.
- Game Development: Functions define the behavior of game objects and characters. Evaluating them determines the game's state at different points in time.
- Machine Learning: Machine learning algorithms often involve evaluating functions to make predictions or classifications.
4. Biology and Medicine:
- Population Growth: Functions model population growth or decay. Evaluating them helps understand population dynamics.
- Drug Dosage: Functions describe the concentration of drugs in the bloodstream over time. Evaluating these functions is crucial for determining appropriate drug dosages.
- Epidemiological Modeling: Functions can model the spread of diseases. Evaluating them aids in predicting the course of epidemics and developing mitigation strategies.
Extending the Concept: Domain and Range
The domain of a function is the set of all possible input values (x-values), and the range is the set of all possible output values (y-values). For the function f(x) = 2x² + 2x + 3, the domain is all real numbers because you can substitute any real number for x. The range, however, is restricted because the parabola opens upwards. The vertex of the parabola represents the minimum value of the function, and the range consists of all values greater than or equal to this minimum value. Finding the vertex requires completing the square or using the formula -b/2a. In this case, the vertex will have a y-coordinate greater than 3 (because of the +3 constant term), indicating that the range is all real numbers greater than or equal to that minimum y-value.
Practical Exercises
To further solidify your understanding, try the following exercises:
- Find f(-2) for the function f(x) = 2x² + 2x + 3.
- Find f(0) for the function f(x) = 2x² + 2x + 3.
- Find f(10) for the function f(x) = 2x² + 2x + 3.
- Consider a function g(x) = x³ - 5x + 2. Find g(2) and g(-1).
By working through these exercises, you'll gain confidence in evaluating functions and applying this crucial concept across various mathematical contexts.
Conclusion
Evaluating a function at a specific point, such as finding f(5) for f(x) = 2x² + 2x + 3, is a fundamental skill in mathematics with far-reaching applications. Understanding this process is crucial for anyone pursuing studies or careers in fields that involve mathematical modeling and analysis. The ability to accurately and efficiently evaluate functions is essential for solving problems, making predictions, and gaining insights from data in various domains. Remember the steps involved: substitute the value into the function, follow the order of operations, and simplify the expression to obtain the result. Practice is key to mastering this important skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Is F 5 For The Function 2x2 2x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.