Which Is Larger 3 4 Or 7 8
News Co
Apr 06, 2025 · 6 min read
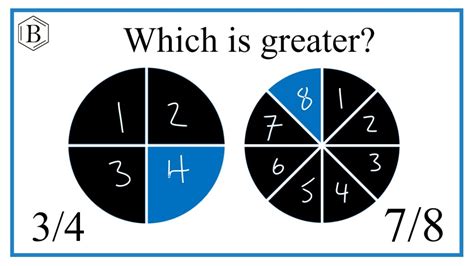
Table of Contents
Which is Larger: 3/4 or 7/8? A Deep Dive into Fraction Comparison
Determining which fraction is larger, 3/4 or 7/8, might seem like a simple task, especially for those comfortable with basic arithmetic. However, understanding the underlying principles behind fraction comparison is crucial for building a strong foundation in mathematics, and for anyone looking to improve their numerical reasoning skills. This article will not only answer the question directly but will also delve into various methods for comparing fractions, providing you with the tools to tackle similar problems with confidence. We'll explore visual representations, common denominators, decimal conversions, and even consider the broader implications of understanding fractional relationships.
Understanding Fractions: A Quick Refresher
Before we jump into comparing 3/4 and 7/8, let's quickly review the fundamentals of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we're considering 3 out of 4 equal parts of a whole.
Method 1: Visual Representation
One of the most intuitive methods for comparing fractions is using visual aids. Imagine two identical circles. Divide the first circle into four equal parts and shade three of them to represent 3/4. Divide the second circle into eight equal parts and shade seven of them to represent 7/8. By visually comparing the shaded areas, it becomes immediately apparent that the shaded portion representing 7/8 is larger than the shaded portion representing 3/4.
This method is particularly helpful for beginners as it provides a concrete, easily understandable representation of the fractions. It's a great way to build an initial understanding before moving on to more abstract methods.
Method 2: Finding a Common Denominator
This is a fundamental method in comparing fractions. The key is to rewrite the fractions so they share the same denominator. This allows for a direct comparison of the numerators.
Let's apply this to our fractions, 3/4 and 7/8. The least common multiple (LCM) of 4 and 8 is 8. Therefore, we need to rewrite 3/4 with a denominator of 8. To do this, we multiply both the numerator and the denominator of 3/4 by 2:
(3 x 2) / (4 x 2) = 6/8
Now we can easily compare 6/8 and 7/8. Since 7 > 6, it's clear that 7/8 is larger than 3/4.
This method is reliable and works for any pair of fractions. Finding the LCM might require some calculation, but it's a systematic approach that guarantees an accurate result. For more complex fractions, understanding prime factorization can significantly simplify the process of finding the LCM.
Method 3: Converting to Decimals
Another effective approach is converting the fractions to decimals. This allows for a direct numerical comparison. To convert a fraction to a decimal, we divide the numerator by the denominator.
3/4 = 0.75
7/8 = 0.875
By comparing the decimal values, we see that 0.875 > 0.75, confirming that 7/8 is larger than 3/4.
This method is particularly useful when dealing with fractions that are difficult to compare using common denominators or when using a calculator. The ease and speed of decimal comparison make this a practical approach for many situations.
Method 4: Cross-Multiplication
Cross-multiplication offers a concise and efficient way to compare fractions. We multiply the numerator of the first fraction by the denominator of the second fraction, and vice-versa. Then we compare the results.
For 3/4 and 7/8:
3 x 8 = 24
7 x 4 = 28
Since 28 > 24, it follows that 7/8 > 3/4.
This method avoids the need to find a common denominator, making it quicker for some comparisons. However, it's essential to remember that this method only provides the relative size of the fractions; it doesn't give you the equivalent fraction with a common denominator.
Understanding the Difference: A Deeper Look
The difference between 7/8 and 3/4 might seem small, but understanding the magnitude of this difference is crucial in various applications, such as calculating proportions, percentages, or working with ratios in real-world problems. The difference is:
7/8 - 3/4 = 7/8 - 6/8 = 1/8
This difference of 1/8 represents 12.5% of the whole. While seemingly insignificant in some contexts, it can be significant in others. For instance, if this represents a portion of a construction material, this difference might impact the structural integrity.
Applications in Real-World Scenarios
The ability to confidently compare fractions is not just an academic exercise. It has practical applications in numerous fields:
-
Cooking and Baking: Following recipes often involves working with fractions of ingredients. Accurately comparing fractions ensures the correct proportions are used.
-
Construction and Engineering: Precise measurements are paramount, and accurately comparing fractions is essential for ensuring structural integrity and functionality.
-
Finance: Calculating interest rates, understanding stock prices, and analyzing financial data often involve working with fractions and percentages.
-
Data Analysis: In statistics and data science, comparing fractions is crucial for interpreting data and drawing meaningful conclusions.
Beyond the Basics: Expanding Your Fraction Skills
Mastering fraction comparison opens doors to more advanced mathematical concepts. Understanding fractions lays the groundwork for:
-
Decimals and Percentages: Fractions, decimals, and percentages are interconnected. Being comfortable with fractions facilitates effortless conversions and manipulations between these three forms.
-
Algebra: Fractions are fundamental building blocks in algebraic equations and expressions.
-
Calculus: Understanding fractions is essential for grasping derivatives and integrals.
-
Probability and Statistics: Fractions and ratios play critical roles in probability calculations and statistical analysis.
Conclusion: Mastering Fractions for a Brighter Future
The simple question of whether 3/4 or 7/8 is larger offers a starting point for a deeper exploration of fractions. By understanding the different methods of comparing fractions—visual representation, common denominators, decimal conversion, and cross-multiplication—you equip yourself with essential mathematical tools applicable in various aspects of life. The ability to confidently work with fractions is not merely a mathematical skill; it's a crucial life skill that enhances problem-solving abilities and opens doors to a wider range of opportunities. Continue practicing and exploring the fascinating world of fractions; the rewards are significant and far-reaching. Remember to always check your work and utilize the method that feels most intuitive and comfortable to you. The important thing is to understand the concepts and apply them consistently.
Latest Posts
Latest Posts
-
How Many Feet Are In A Tenth Of A Mile
Apr 07, 2025
-
Volume Of A Rectangular Based Pyramid
Apr 07, 2025
-
How Many Vertices Does A Trapezium Have
Apr 07, 2025
-
Are The Diagonals Of A Parallelogram Perpendicular
Apr 07, 2025
-
Place Value Worksheets For 5th Graders
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Which Is Larger 3 4 Or 7 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
