Which Number Is A Factor Of 51
News Co
Apr 18, 2025 · 6 min read
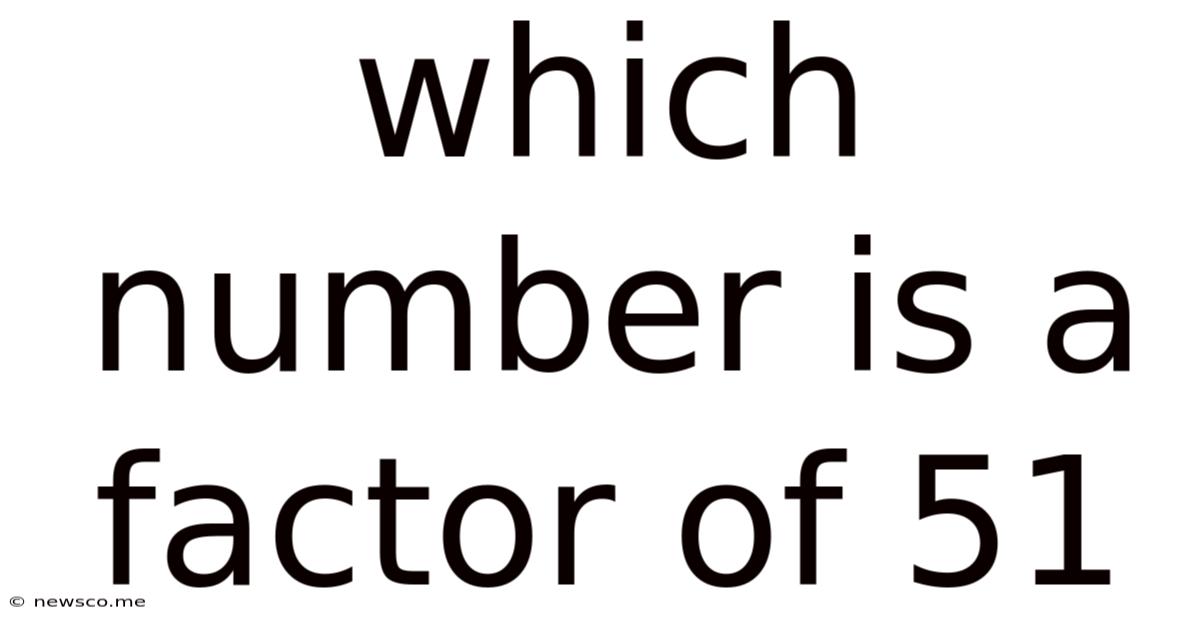
Table of Contents
Which Number is a Factor of 51? A Deep Dive into Divisibility and Prime Factorization
Finding the factors of a number might seem like a simple arithmetic task, but it's a fundamental concept in mathematics with far-reaching implications in various fields, including cryptography and computer science. This article delves into the question: Which number is a factor of 51? We'll explore the meaning of factors, methods for finding them, and demonstrate how understanding factors contributes to a broader understanding of number theory.
Understanding Factors and Divisibility
Before we identify the factors of 51, let's establish a clear understanding of what a factor is. A factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. In other words, if 'a' is a factor of 'b', then b/a results in a whole number. This concept is intimately linked to divisibility: a number is divisible by another number if the result of their division is a whole number.
For example, consider the number 12. Its factors are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Finding Factors of 51: A Systematic Approach
Several methods can be used to find the factors of 51. Let's explore the most common and effective techniques:
1. Trial Division
The simplest method is trial division. We systematically test each whole number, starting from 1, to see if it divides 51 without a remainder.
- 1: 51 ÷ 1 = 51 (Remainder 0) - 1 is a factor.
- 2: 51 ÷ 2 = 25.5 (Remainder 0.5) - 2 is not a factor.
- 3: 51 ÷ 3 = 17 (Remainder 0) - 3 is a factor.
- 4: 51 ÷ 4 = 12.75 (Remainder 0.75) - 4 is not a factor.
- 5: 51 ÷ 5 = 10.2 (Remainder 0.2) - 5 is not a factor.
- 6: 51 ÷ 6 = 8.5 (Remainder 0.5) - 6 is not a factor.
- 7: 51 ÷ 7 ≈ 7.29 (Remainder ≈ 0.29) - 7 is not a factor.
- 8: 51 ÷ 8 ≈ 6.375 (Remainder ≈ 0.375) - 8 is not a factor.
- 9: 51 ÷ 9 ≈ 5.67 (Remainder ≈ 0.67) - 9 is not a factor.
- 10: 51 ÷ 10 = 5.1 (Remainder 0.1) - 10 is not a factor.
- 11: 51 ÷ 11 ≈ 4.64 (Remainder ≈ 0.64) - 11 is not a factor.
- 12: 51 ÷ 12 ≈ 4.25 (Remainder ≈ 0.25) - 12 is not a factor.
- 13: 51 ÷ 13 ≈ 3.92 (Remainder ≈ 0.08) - 13 is not a factor.
- 14: 51 ÷ 14 ≈ 3.64 (Remainder ≈ 0.36) - 14 is not a factor.
- 15: 51 ÷ 15 = 3.4 (Remainder 0.6) - 15 is not a factor.
- 16: 51 ÷ 16 ≈ 3.1875 (Remainder ≈ 0.1875) - 16 is not a factor.
- 17: 51 ÷ 17 = 3 (Remainder 0) - 17 is a factor.
We can stop here because we've reached 17, which is less than the square root of 51 (approximately 7.14). Any factor larger than 17 will have a corresponding factor smaller than 17 that we've already tested.
2. Prime Factorization
A more efficient approach for larger numbers involves prime factorization. This method breaks down a number into its prime factors – prime numbers that, when multiplied together, give the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
51 can be factored as 3 x 17. Both 3 and 17 are prime numbers. Therefore, the factors of 51 are 1, 3, 17, and 51.
Understanding the Significance of Factors
The concept of factors extends beyond simple arithmetic exercises. It plays a crucial role in:
1. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Factors are essential for calculating the GCD and LCM of two or more numbers. The GCD is the largest number that divides all the given numbers without leaving a remainder. The LCM is the smallest number that is a multiple of all the given numbers. These concepts are frequently used in simplifying fractions, solving problems in algebra, and various other mathematical applications.
2. Number Theory and Cryptography
Understanding factors is fundamental in number theory, a branch of mathematics dealing with the properties of integers. Prime factorization, in particular, underpins many cryptographic algorithms used for secure communication and data protection. RSA encryption, one of the most widely used public-key cryptosystems, relies heavily on the difficulty of factoring large numbers into their prime components.
3. Computer Science and Algorithm Design
Factorization algorithms are integral to computer science, particularly in areas like algorithm design and optimization. The efficiency of these algorithms influences the speed and performance of various computational processes.
Factors of 51: A Summary
To reiterate, the factors of 51 are 1, 3, 17, and 51. These numbers divide 51 exactly without leaving a remainder. Understanding how to find factors, whether through trial division or prime factorization, is a valuable skill that extends far beyond basic arithmetic, impacting various fields of mathematics and computer science. The seemingly simple question, "Which number is a factor of 51?" opens a door to a deeper exploration of number theory and its practical applications.
Further Exploration: Beyond the Basics
While we've addressed the primary question, let's delve into some related concepts that broaden our understanding:
1. Perfect Numbers
A perfect number is a positive integer that is equal to the sum of its proper divisors (divisors excluding the number itself). For example, 6 is a perfect number because its proper divisors (1, 2, 3) sum up to 6 (1 + 2 + 3 = 6). Exploring perfect numbers provides insight into the fascinating relationships between numbers and their divisors.
2. Abundant and Deficient Numbers
Abundant numbers have the sum of their proper divisors greater than the number itself, while deficient numbers have the sum of their proper divisors less than the number itself. These classifications provide further categorization within the broader study of divisors.
3. Divisibility Rules
Divisibility rules provide shortcuts for determining whether a number is divisible by certain numbers without performing the actual division. For instance, a number is divisible by 3 if the sum of its digits is divisible by 3. Learning these rules enhances efficiency in factor finding and number analysis.
4. Modular Arithmetic
Modular arithmetic involves performing arithmetic operations within a specified range (a modulus). This system has profound implications in cryptography and other areas where cyclical patterns are relevant. Understanding factors is crucial for working effectively with modular arithmetic.
Conclusion: The Enduring Importance of Factors
The seemingly simple task of finding the factors of 51 leads us to a deeper appreciation of the rich and complex world of number theory. The ability to identify factors is a fundamental skill with far-reaching consequences in various scientific and technological fields. By exploring the concepts discussed in this article, we hope to have provided a comprehensive understanding of factors, their significance, and their applications. Remember, the journey of mathematical exploration is endless, and every number holds within it a universe of interesting properties waiting to be discovered.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Number Is A Factor Of 51 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.