Which Points Are Solutions To The Linear Inequality Y 0.5x+2
News Co
Mar 19, 2025 · 5 min read
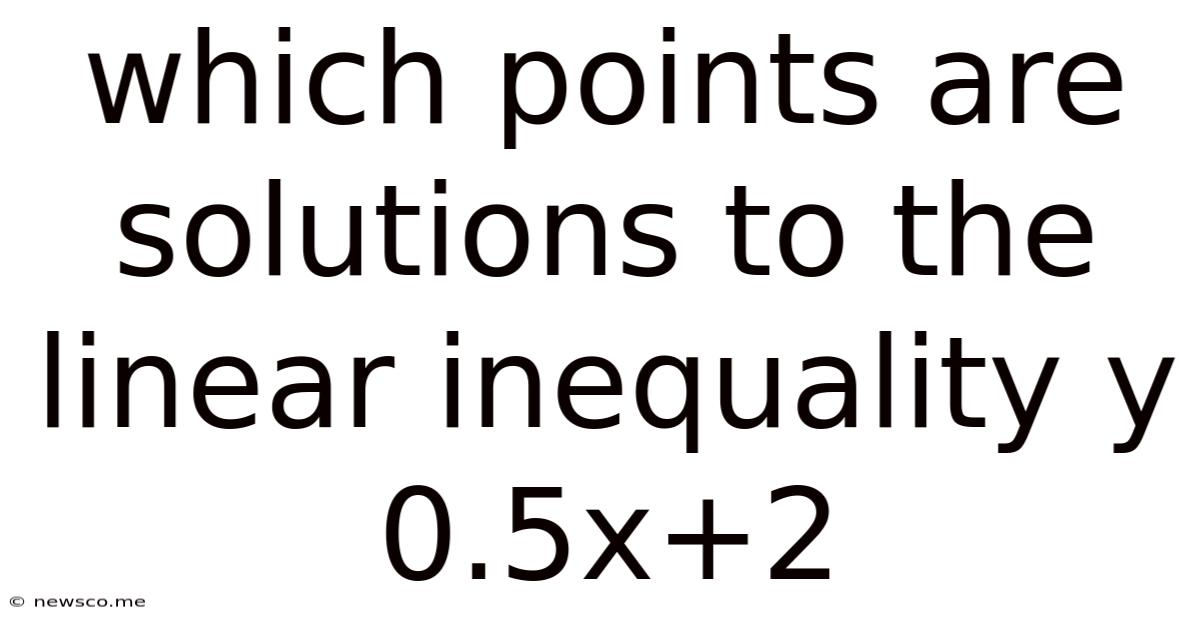
Table of Contents
Which Points are Solutions to the Linear Inequality y < 0.5x + 2? A Comprehensive Guide
Understanding linear inequalities is crucial in various fields, from mathematics and computer science to economics and engineering. This article delves deep into the linear inequality y < 0.5x + 2, explaining how to identify points that satisfy this inequality and providing a comprehensive understanding of the solution set. We will explore graphical and algebraic methods, and cover advanced concepts to solidify your grasp of this topic.
Understanding the Inequality y < 0.5x + 2
The inequality y < 0.5x + 2 represents a half-plane in a two-dimensional Cartesian coordinate system. It signifies all the points (x, y) where the y-coordinate is strictly less than 0.5 times the x-coordinate plus 2. The expression 0.5x + 2 defines a straight line, and the inequality specifies the region below this line. The line itself is not included in the solution set because of the "less than" symbol (<), not "less than or equal to" (≤).
Key Components of the Inequality
y: The dependent variable, whose value depends on the value ofx.x: The independent variable. You can choose any value forx.0.5: The slope of the line. This indicates that for every one-unit increase inx,yincreases by 0.5 units.2: The y-intercept. This is the point where the line intersects the y-axis (when x = 0).<: The inequality symbol, indicating that the solution set includes all points below the liney = 0.5x + 2.
Graphical Method for Identifying Solutions
The most intuitive way to visualize the solution set is by graphing the inequality.
1. Graphing the Line y = 0.5x + 2
First, graph the line y = 0.5x + 2. You can do this by finding two points on the line:
- When x = 0: y = 0.5(0) + 2 = 2. So, one point is (0, 2).
- When x = 2: y = 0.5(2) + 2 = 3. So, another point is (2, 3).
Plot these points and draw a straight line through them. Remember to draw a dashed line because the inequality is strictly less than, meaning points on the line are not part of the solution.
2. Shading the Solution Region
Since the inequality is y < 0.5x + 2, the solution set includes all points below the dashed line. Shade this region to clearly represent the solution set. Any point within the shaded area will satisfy the inequality.
3. Testing Points
To verify your graph, you can test points from both the shaded region and the unshaded region. Let's test a few:
- Point (0, 0): Substituting into the inequality: 0 < 0.5(0) + 2 => 0 < 2. This is true, so (0, 0) is a solution. This aligns with our shaded region.
- Point (2, 4): Substituting: 4 < 0.5(2) + 2 => 4 < 3. This is false, so (2, 4) is not a solution. This point lies above the line, confirming our shaded region.
- Point (4, 0): Substituting: 0 < 0.5(4) + 2 => 0 < 4. This is true, so (4,0) is a solution.
Algebraic Method for Identifying Solutions
The graphical method provides a visual understanding, but the algebraic method allows for precise determination of whether a point is a solution. Simply substitute the x and y coordinates of the point into the inequality. If the inequality holds true, the point is a solution; otherwise, it's not.
Example: Testing Point (3, 1)
Let's test if the point (3, 1) is a solution:
- Substitute x = 3 and y = 1 into the inequality:
1 < 0.5(3) + 2 - Simplify:
1 < 3.5 - The inequality is true. Therefore, (3, 1) is a solution to the inequality
y < 0.5x + 2.
Example: Testing Point (1, 3)
Let's test if the point (1, 3) is a solution:
- Substitute x = 1 and y = 3 into the inequality:
3 < 0.5(1) + 2 - Simplify:
3 < 2.5 - The inequality is false. Therefore, (1, 3) is not a solution to the inequality
y < 0.5x + 2.
Advanced Concepts and Applications
Understanding the solution set of y < 0.5x + 2 opens doors to more complex scenarios.
1. Systems of Inequalities
You might encounter situations involving multiple inequalities. For example, consider the system:
y < 0.5x + 2
y > -x + 1
The solution to this system is the region where both inequalities are true – the overlapping area of the shaded regions for each individual inequality.
2. Optimization Problems
Linear inequalities are fundamental to linear programming, a powerful technique used to optimize objectives (like maximizing profit or minimizing cost) subject to constraints (represented by inequalities).
3. Real-World Applications
Linear inequalities model numerous real-world phenomena:
- Resource allocation: Determining the optimal allocation of resources (e.g., materials, labor) given constraints on availability.
- Production planning: Planning production levels to meet demand while adhering to resource limitations.
- Financial modeling: Analyzing investment portfolios and managing risk.
- Scheduling problems: Optimizing schedules for tasks or events with time constraints.
Identifying Boundary Points
While the line y = 0.5x + 2 itself is not part of the solution set, understanding points on the line is crucial for defining the boundary of the solution region. These boundary points help us visualize the extent of the solution set. Any point directly on the line y = 0.5x + 2 will make the inequality y < 0.5x + 2 false.
Determining points on the line:
To find points on the line, simply substitute various values of 'x' into the equation y = 0.5x + 2 and calculate the corresponding 'y' values. For example:
- If x = 4, y = 0.5(4) + 2 = 4. The point (4, 4) lies on the line.
- If x = -2, y = 0.5(-2) + 2 = 1. The point (-2, 1) lies on the line.
These points define the boundary separating the solution set from the non-solution set.
Conclusion: Mastering Linear Inequalities
Understanding how to determine which points satisfy the linear inequality y < 0.5x + 2 is essential for various mathematical and real-world applications. By combining graphical and algebraic methods, you can confidently identify solutions and visualize the solution set. Remember that the solution set is the region below the line y = 0.5x + 2, excluding the line itself. Furthermore, understanding boundary points allows for a complete comprehension of the solution region's boundaries and extent. The concepts explored here provide a strong foundation for tackling more complex problems involving systems of inequalities and optimization. With practice, you'll become proficient in analyzing and solving linear inequalities, unlocking their power in various applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Points Are Solutions To The Linear Inequality Y 0.5x+2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.