Which Polynomial Is Prime X 3 3x 2 2x 6
News Co
Mar 27, 2025 · 4 min read
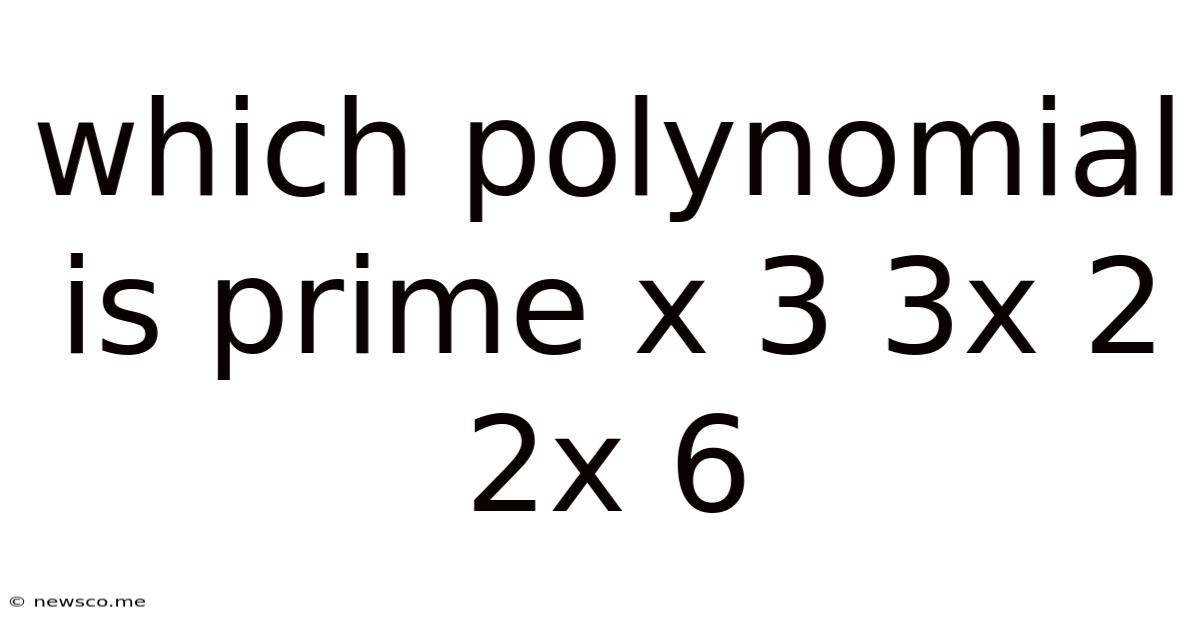
Table of Contents
Is the Polynomial x³ + 3x² + 2x + 6 Prime? A Deep Dive into Polynomial Factorization
Determining whether a polynomial is prime (irreducible) is a fundamental concept in algebra. Unlike integers, where primality is straightforward, polynomial primality depends on the field over which we consider the polynomial. This article delves into the question of whether the polynomial x³ + 3x² + 2x + 6 is prime, exploring various techniques and providing a comprehensive understanding of the process.
Understanding Polynomial Primality
A polynomial is considered prime (or irreducible) if it cannot be factored into non-constant polynomials of lower degree within a given field. The field in question is crucial; a polynomial might be irreducible over one field but reducible over another. For example, x² + 1 is irreducible over the real numbers (ℝ) but reducible over the complex numbers (ℂ) as it factors into (x + i)(x - i).
Methods for Testing Polynomial Primality
Several methods exist for determining whether a polynomial is prime. The most common include:
- Rational Root Theorem: This theorem helps identify potential rational roots of a polynomial. If a rational root exists, the polynomial is reducible.
- Eisenstein's Criterion: This powerful criterion provides a sufficient (but not necessary) condition for irreducibility.
- Modulus Tests: Examining the polynomial's behavior modulo a prime number can reveal information about its reducibility.
- Direct Factorization Attempts: This involves systematically trying to factor the polynomial. While less systematic than the other methods, it can be effective for lower-degree polynomials.
Analyzing x³ + 3x² + 2x + 6
Let's apply these methods to the polynomial P(x) = x³ + 3x² + 2x + 6.
1. Rational Root Theorem
The Rational Root Theorem states that any rational root of a polynomial with integer coefficients must be of the form p/q, where p is a divisor of the constant term and q is a divisor of the leading coefficient. In our case:
- Constant term: 6 (divisors: ±1, ±2, ±3, ±6)
- Leading coefficient: 1 (divisors: ±1)
Therefore, the potential rational roots are ±1, ±2, ±3, ±6. Let's test them:
- P(1) = 1 + 3 + 2 + 6 = 12 ≠ 0
- P(-1) = -1 + 3 - 2 + 6 = 6 ≠ 0
- P(2) = 8 + 12 + 4 + 6 = 30 ≠ 0
- P(-2) = -8 + 12 - 4 + 6 = 6 ≠ 0
- P(3) = 27 + 27 + 6 + 6 = 66 ≠ 0
- P(-3) = -27 + 27 - 6 + 6 = 0
We found that x = -3 is a root. This means (x + 3) is a factor. We can perform polynomial long division to find the other factor:
(x³ + 3x² + 2x + 6) / (x + 3) = x² + 2
Therefore, x³ + 3x² + 2x + 6 = (x + 3)(x² + 2).
2. Eisenstein's Criterion
Eisenstein's Criterion states that if there exists a prime number p such that:
- p divides all coefficients except the leading coefficient.
- p² does not divide the constant term.
Then the polynomial is irreducible over the rational numbers.
In our case, no such prime number exists. Therefore, Eisenstein's Criterion doesn't directly help us determine irreducibility. However, we've already factored the polynomial, demonstrating its reducibility.
3. Modulus Tests
Let's examine the polynomial modulo a prime number, say p = 2:
P(x) ≡ x³ + x² (mod 2)
This reduced polynomial is not easily factored modulo 2, but it doesn't directly prove irreducibility.
4. Direct Factorization
We already successfully factored the polynomial using the rational root theorem and polynomial long division.
Conclusion: x³ + 3x² + 2x + 6 is Reducible
Based on our analysis, particularly the successful application of the Rational Root Theorem, we definitively conclude that the polynomial x³ + 3x² + 2x + 6 is reducible over the rational numbers (ℚ). It factors into (x + 3)(x² + 2). Note that x² + 2 is irreducible over ℚ but reducible over ℂ, factoring into (x + i√2)(x - i√2).
Further Exploration: Fields and Irreducibility
The concept of polynomial primality is deeply connected to the field over which the polynomial is defined. A polynomial irreducible over one field might be reducible over an extension field. This highlights the importance of specifying the field when discussing polynomial irreducibility.
For instance, consider the polynomial x² + 1. It's irreducible over the real numbers (ℝ), but reducible over the complex numbers (ℂ), factoring into (x + i)(x - i). This emphasizes the critical role of the underlying field in determining a polynomial's irreducibility.
Practical Applications of Polynomial Factorization
The ability to factor polynomials is crucial in various mathematical and scientific applications, including:
- Solving Polynomial Equations: Factoring a polynomial allows us to easily find its roots.
- Partial Fraction Decomposition: This technique, used extensively in calculus and other fields, relies on factoring polynomials in the denominator.
- Signal Processing: Polynomial factorization plays a role in digital signal processing algorithms.
- Control Systems Engineering: Polynomial factorization is essential in the analysis and design of control systems.
- Cryptography: Polynomial factorization underlies certain cryptographic algorithms.
Understanding the techniques for determining polynomial primality is a foundational skill for anyone working in these areas. The seemingly simple question of whether a polynomial is prime reveals the rich depth and interconnectedness of algebraic concepts. The case of x³ + 3x² + 2x + 6 serves as an excellent example of how different methods can be employed to arrive at a definitive conclusion about reducibility.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Polynomial Is Prime X 3 3x 2 2x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.