Which Square Root Is Between 4 And 5
News Co
May 09, 2025 · 5 min read
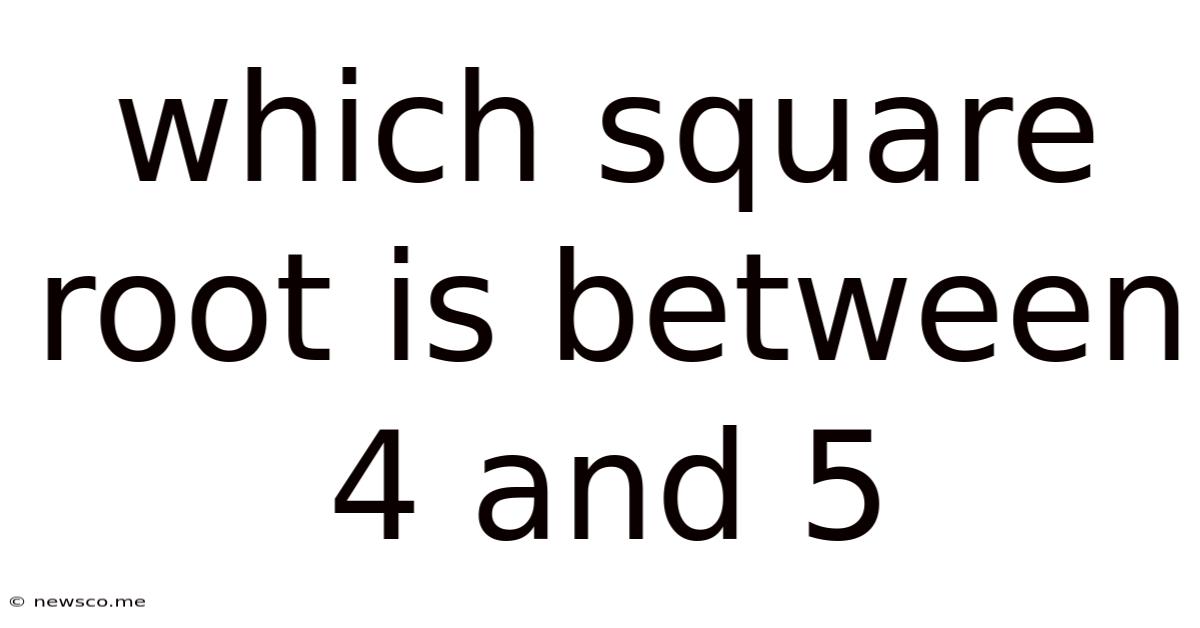
Table of Contents
Which Square Root is Between 4 and 5? A Deep Dive into Square Roots and Number Systems
Finding a square root that falls between 4 and 5 might seem like a simple mathematical problem, but it opens a fascinating door into the world of numbers, their properties, and the elegance of mathematical systems. This exploration goes beyond a simple answer; we'll delve into the nature of square roots, irrational numbers, and their representation within various number systems.
Understanding Square Roots
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This concept is fundamental to algebra and many other mathematical disciplines.
Perfect Squares vs. Non-Perfect Squares
Numbers like 9, 16, 25, and so on are called perfect squares because their square roots are whole numbers (integers). However, many numbers don't have whole number square roots. These are called non-perfect squares. Our quest – finding a square root between 4 and 5 – falls squarely (pun intended!) into this category.
The Number Line and Square Roots
Visualizing numbers on a number line helps us understand their relationships. The square root of 16 (√16 = 4) sits precisely at the point 4. Similarly, √25 = 5 sits at point 5. Our mystery number lies somewhere between these two points on the number line.
Identifying the Square Root Between 4 and 5
Since we're looking for a number whose square is between 16 and 25, we can approach this problem through various methods:
1. Estimation and Trial and Error
Let's start with a guess. A number halfway between 4 and 5 is 4.5. If we square 4.5 (4.5 x 4.5 = 20.25), we see it falls between 16 and 25. Therefore, the square root of 20.25 is between 4 and 5. This is a simple but effective method, especially for estimations. However, it doesn't always provide an exact answer.
2. Using a Calculator
Modern calculators readily provide square roots. Inputting the numbers between 16 and 25, we'll find that only the square root of 20.25 falls within our desired range. This method gives us the precise answer quickly, but it lacks the deeper understanding gained from other approaches.
3. Babylonian Method (or Heron's Method)
This ancient iterative method provides a remarkably accurate approximation of square roots. Let's use it to find the square root of 20:
- Make an initial guess: Let's guess 4.5.
- Improve the guess: Divide the number (20) by our guess (4.5), and then average the result with the original guess: (20/4.5 + 4.5) / 2 ≈ 4.472
- Iterate: Repeat step 2 using the new guess. The more iterations, the closer we get to the true value.
This method demonstrates how successive approximations can lead to a highly accurate result. While computationally intensive without a calculator, it showcases a powerful algorithmic approach to solving square root problems.
Delving into Irrational Numbers
Our quest reveals an important class of numbers: irrational numbers. These numbers cannot be expressed as a simple fraction (a ratio of two integers). The square root of 20, for example, is an irrational number. Its decimal representation continues infinitely without repeating. This is in contrast to rational numbers, which can be expressed as fractions, such as 1/2, 3/4, or 4.5.
Representing Irrational Numbers
The infinite nature of irrational numbers poses a challenge for precise representation. We can use:
- Decimal approximations: We can round the square root of 20 to a certain number of decimal places (e.g., 4.4721), but this introduces a degree of inaccuracy.
- Continued fractions: These represent numbers as a series of fractions within fractions, offering a unique and precise, though not easily intuitive, representation.
- Symbolic representation: Using the radical symbol (√) provides an exact representation, even if we can't write out its decimal expansion completely.
Expanding the Understanding: Beyond the Specific Case
Let's generalize our understanding beyond the specific problem of finding a square root between 4 and 5. This problem helps illustrate several broader mathematical concepts:
The Density of Real Numbers
The fact that we can find a square root between any two integers highlights the density of real numbers. Between any two real numbers, no matter how close, there are infinitely many other real numbers. This infinite density is a defining characteristic of the real number system.
Number System Hierarchy
Our exploration touches upon the hierarchy of number systems:
- Natural numbers: 1, 2, 3...
- Integers: ..., -2, -1, 0, 1, 2...
- Rational numbers: Numbers expressible as fractions.
- Irrational numbers: Numbers not expressible as fractions.
- Real numbers: The union of rational and irrational numbers.
Understanding this hierarchy provides a clearer picture of the relationships between different types of numbers.
Applications of Square Roots
Square roots are not merely abstract mathematical concepts; they have numerous applications across diverse fields:
- Physics: Calculating distances, velocities, and accelerations.
- Engineering: Designing structures, calculating forces, and analyzing vibrations.
- Computer Graphics: Generating 2D and 3D images and animations.
- Finance: Calculating compound interest and determining investment returns.
Conclusion: The Significance of a Simple Problem
The seemingly simple question of finding a square root between 4 and 5 unveils a wealth of mathematical depth. From understanding perfect and non-perfect squares to grappling with the nature of irrational numbers and the density of the real number system, this problem serves as a springboard for exploring fundamental mathematical principles and their far-reaching applications. This deep dive emphasizes the interconnectedness of mathematical concepts and the power of simple questions to unlock a wider understanding of the mathematical world. The answer, while easily obtainable with a calculator, is far more significant in the context of broader mathematical understanding. It acts as a microcosm of the beauty and complexity inherent in the field of mathematics. The exploration of this seemingly simple problem highlights the rich tapestry woven from seemingly simple numerical relationships, underscoring the enduring fascination and importance of mathematical exploration.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Which Square Root Is Between 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.