Write 13/12 As A Mixed Number
News Co
Mar 21, 2025 · 5 min read
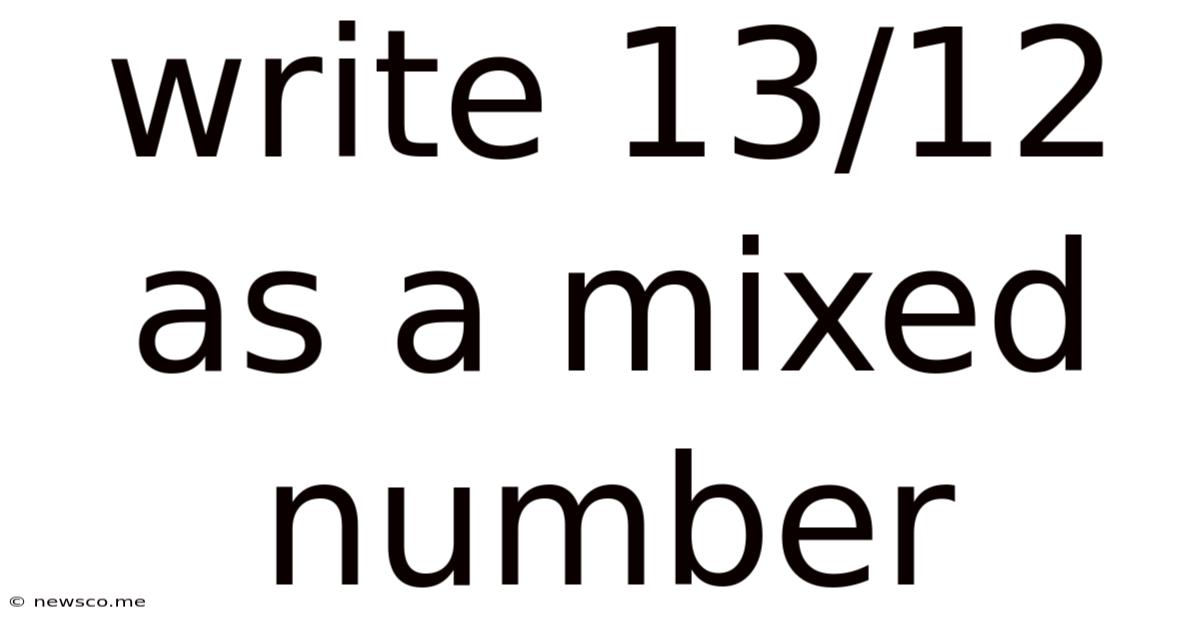
Table of Contents
Writing 13/12 as a Mixed Number: A Comprehensive Guide
The seemingly simple task of converting an improper fraction like 13/12 into a mixed number holds a significant place in foundational mathematics. Understanding this conversion is crucial for moving beyond basic arithmetic and tackling more complex mathematical concepts. This comprehensive guide will not only show you how to convert 13/12 to a mixed number but will also delve into the underlying principles, provide various methods, and explore practical applications. We'll also touch upon related concepts to solidify your understanding.
Understanding Fractions: A Quick Recap
Before we dive into the conversion process, let's briefly revisit the fundamental concepts of fractions. A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, representing the number of parts we have.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into.
In the fraction 13/12, 13 is the numerator and 12 is the denominator. This means we have 13 parts out of a total of 12 equal parts. This is an improper fraction because the numerator (13) is greater than the denominator (12). Improper fractions always represent a value greater than one.
Converting 13/12 to a Mixed Number: The Core Process
A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). Converting an improper fraction to a mixed number involves determining how many whole units are contained within the improper fraction and then expressing the remaining part as a proper fraction.
Here's how to convert 13/12 to a mixed number:
-
Division: Divide the numerator (13) by the denominator (12).
13 ÷ 12 = 1 with a remainder of 1
-
Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 1.
-
Proper Fraction: The remainder (1) becomes the numerator of the proper fraction, and the original denominator (12) remains the denominator. This gives us the proper fraction 1/12.
-
Mixed Number: Combine the whole number and the proper fraction to form the mixed number.
Therefore, 13/12 = 1 1/12
Alternative Methods for Conversion
While the division method is the most straightforward, other approaches can help solidify your understanding and offer alternative perspectives:
Method 2: Visual Representation
Imagine you have 13 pizzas, each cut into 12 slices. You can easily assemble 1 full pizza (12 slices) from these slices. You'll have 1 slice remaining. This remaining slice represents 1/12 of a pizza. Thus, you have 1 whole pizza and 1/12 of a pizza, represented as 1 1/12.
Method 3: Repeated Subtraction
Repeatedly subtract the denominator from the numerator until the result is less than the denominator. The number of times you subtracted is the whole number, and the remaining value is the numerator of the proper fraction.
13 - 12 = 1
We subtracted 12 once, so the whole number is 1. The remainder is 1, which becomes the numerator of the proper fraction, resulting in 1 1/12.
Why Convert to Mixed Numbers?
Converting improper fractions to mixed numbers often makes it easier to:
-
Visualize Quantities: Mixed numbers provide a clearer picture of the quantity represented compared to improper fractions, especially in real-world applications. For example, "1 1/12 pizzas" is more intuitive than "13/12 pizzas."
-
Simplify Calculations: In some calculations, mixed numbers are simpler to work with than improper fractions. Adding and subtracting mixed numbers can sometimes be more intuitive than working with improper fractions.
-
Understand Comparisons: Comparing mixed numbers is often easier than comparing improper fractions. It's readily apparent that 1 1/12 is greater than 1, for instance.
Practical Applications of Mixed Numbers
Mixed numbers appear frequently in everyday life and various fields:
-
Cooking and Baking: Recipes often use mixed numbers to represent quantities of ingredients (e.g., 2 1/2 cups of flour).
-
Measurement: Measurements of length, weight, and volume frequently involve mixed numbers (e.g., 5 3/4 inches).
-
Construction and Engineering: Precise measurements in construction and engineering often require the use of mixed numbers.
-
Time: Time is often expressed using mixed numbers (e.g., 1 1/2 hours).
-
Data Analysis: In data analysis, mixed numbers can represent averages or proportions.
Expanding on Fraction Concepts: Equivalent Fractions
Understanding equivalent fractions is essential for working with fractions effectively. Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/2, 2/4, 3/6, and 6/12 are all equivalent fractions. They all represent one-half.
You can find equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number.
Expanding on Fraction Concepts: Simplifying Fractions
Simplifying fractions, also known as reducing fractions to their lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. For instance, the fraction 6/12 can be simplified to 1/2 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 6. This simplifies the fraction while maintaining its value.
Addressing Potential Challenges and Common Mistakes
While converting improper fractions to mixed numbers is relatively straightforward, some common mistakes should be avoided:
-
Incorrect Division: Ensure you perform the division correctly. A simple mistake in division can lead to an incorrect mixed number.
-
Misinterpreting Remainders: The remainder should always become the numerator of the proper fraction.
-
Forgetting the Whole Number: Remember to include the whole number part of the mixed number in your final answer.
-
Not Simplifying the Proper Fraction: Always simplify the proper fraction to its lowest terms if possible.
Conclusion: Mastering the Conversion
Converting the improper fraction 13/12 to the mixed number 1 1/12 is a fundamental skill in mathematics. This process, while seemingly simple, underpins a deeper understanding of fractions and their various applications. By mastering this conversion and grasping the related concepts of equivalent and simplified fractions, you'll build a strong foundation for more advanced mathematical work. Remember to practice regularly to reinforce your understanding and improve your proficiency. The more you work with fractions, the more comfortable and confident you will become. Through understanding the different methods and practical applications, you can confidently navigate the world of fractions and utilize this knowledge in diverse contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Write 13/12 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.