Write Two Fractions Equivalent To 9/12
News Co
Mar 28, 2025 · 5 min read
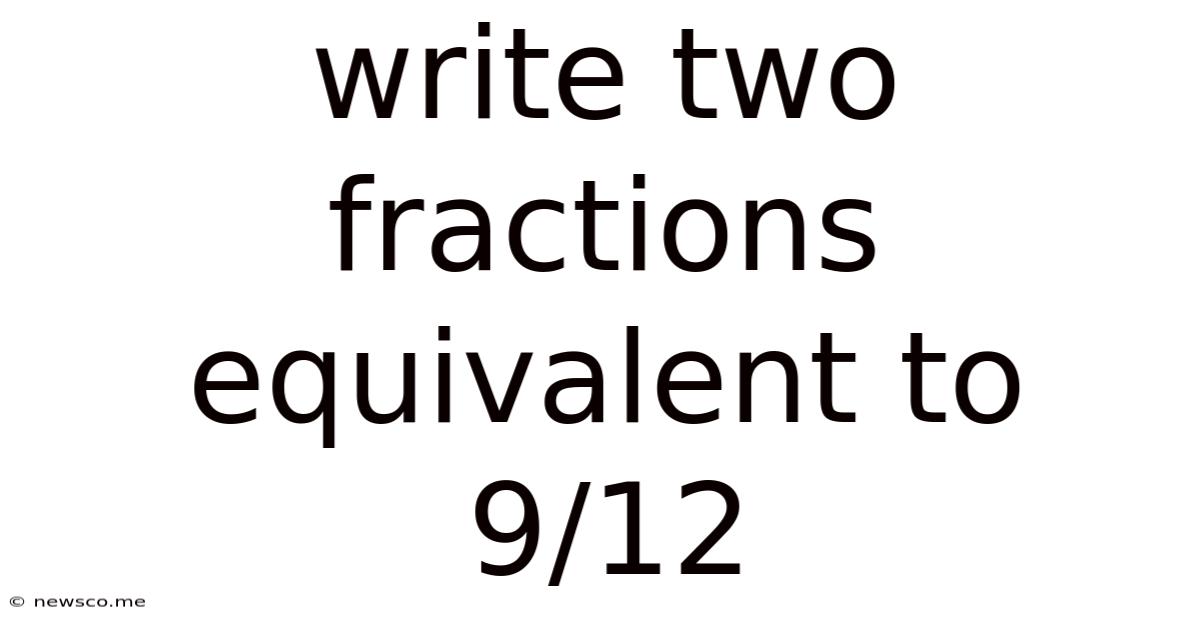
Table of Contents
Finding Equivalent Fractions: Two Fractions Equivalent to 9/12
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding proportions, ratios, and simplifying complex expressions. This article delves deep into the process of finding equivalent fractions, using the example of 9/12. We'll explore multiple methods, explain the underlying principles, and provide ample examples to solidify your understanding. Beyond simply finding two equivalent fractions, we’ll explore the broader implications of this concept and its applications in various mathematical contexts.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. Think of a pizza: cutting a pizza into 12 slices and taking 9 represents the same amount as cutting a pizza into 6 slices and taking 6. Both represent ¾ of the pizza. The key is that the ratio between the numerator (top number) and the denominator (bottom number) remains constant. To find an equivalent fraction, you need to multiply or divide both the numerator and the denominator by the same non-zero number.
Method 1: Simplifying 9/12 (Finding the Simplest Form)
The simplest form of a fraction is when the numerator and the denominator have no common factors other than 1. This process is called simplification or reducing the fraction to its lowest terms.
To simplify 9/12, we find the greatest common divisor (GCD) of 9 and 12. The GCD is the largest number that divides both 9 and 12 without leaving a remainder. In this case, the GCD is 3.
We divide both the numerator and the denominator by the GCD:
9 ÷ 3 = 3 12 ÷ 3 = 4
Therefore, the simplest form of 9/12 is 3/4. This is one of our equivalent fractions.
Finding the Prime Factorization (Alternative Approach to Finding GCD)
An alternative way to find the GCD is through prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors.
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
The common prime factor is 3. Therefore, the GCD is 3.
Method 2: Multiplying the Numerator and Denominator
To find another equivalent fraction, we can multiply both the numerator and the denominator of 9/12 (or its simplified form, 3/4) by the same number. Let's choose 2:
-
Starting with 9/12:
- 9 x 2 = 18
- 12 x 2 = 24 Therefore, 18/24 is an equivalent fraction to 9/12.
-
Starting with 3/4:
- 3 x 2 = 6
- 4 x 2 = 8 Therefore, 6/8 is also an equivalent fraction to 9/12.
Let's try multiplying by 5:
- Starting with 3/4:
- 3 x 5 = 15
- 4 x 5 = 20 Therefore, 15/20 is another equivalent fraction.
As you can see, there are infinitely many equivalent fractions for any given fraction. You can generate as many as you need by multiplying the numerator and denominator by any non-zero integer.
Visual Representation of Equivalent Fractions
Visualizing equivalent fractions using shapes or diagrams can be incredibly helpful, especially for beginners. Imagine a rectangle divided into 12 equal parts, with 9 parts shaded. This represents 9/12. Now, imagine dividing that same rectangle into 6 equal parts by combining pairs of the original 12 parts. You'll find that 6 out of 6 are shaded, representing 6/6, which is equivalent to 9/12. Similarly, you could divide the rectangle into 4 equal parts, representing 3/4, which is also equivalent.
Applications of Equivalent Fractions
Understanding equivalent fractions is crucial for various mathematical applications:
- Simplifying fractions: Reducing fractions to their simplest form makes calculations easier and more efficient.
- Comparing fractions: Finding equivalent fractions with a common denominator makes it easier to compare the size of different fractions.
- Adding and subtracting fractions: To add or subtract fractions, you need to find equivalent fractions with a common denominator.
- Solving proportions: Proportions involve equal ratios, and equivalent fractions are essential in solving proportion problems.
- Working with percentages: Percentages are essentially fractions with a denominator of 100. Converting fractions to percentages often involves finding equivalent fractions.
- Real-world applications: From cooking (measuring ingredients) to construction (measuring materials) to finance (calculating interest), understanding fractions is vital.
Beyond the Basics: Exploring More Complex Scenarios
While we've focused on finding two equivalent fractions for 9/12, the principles extend to more complex situations. Consider finding equivalent fractions with larger denominators, or working with fractions involving decimals or mixed numbers. The core concepts remain the same: maintain the ratio between the numerator and denominator by multiplying or dividing both by the same non-zero number.
For example, if you need to find an equivalent fraction of 9/12 with a denominator of 48, you would ask: "What number multiplied by 12 gives 48?" The answer is 4. Therefore, multiply both the numerator and denominator of 9/12 by 4:
9 x 4 = 36 12 x 4 = 48
The equivalent fraction is 36/48.
Conclusion: Mastering Equivalent Fractions
Mastering equivalent fractions is a cornerstone of mathematical proficiency. By understanding the principles of simplification and multiplication, you can confidently find equivalent fractions for any given fraction and apply this knowledge to various mathematical problems and real-world situations. Remember that the key is to maintain the ratio between the numerator and the denominator, ensuring you're working with the same value, only expressed differently. This skill is foundational and will support your progress in more advanced mathematical concepts. Practice makes perfect – so keep practicing and solidifying your understanding!
Latest Posts
Related Post
Thank you for visiting our website which covers about Write Two Fractions Equivalent To 9/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.